题目内容
14.计算:${(1-\sqrt{3})}^{0}$+|-2|-2cos45°+${(\frac{1}{4})}^{-1}$.分析 利用负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值分别化简得出答案.
解答 解:原式=1+2-2×$\frac{\sqrt{2}}{2}$+4
=7-$\sqrt{2}$.
点评 此题主要考查了负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值等知识,正确化简各数是解题关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
4.某工厂生产的一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长x(单位:cm)在5到50之间(含5和50),每张薄板的出场价y(单位:元)由基础价a和浮动价b两部分组成,其中基础价与薄板的大小无关,是固定不变的.浮动价b与薄板的边长x成正比例.在营销过程中得到了表格中的数据.
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)每张薄板的成本价w(单位:元)与它的面积x2(单位:cm2)成正比例,已知出厂一张边长为40cm的薄板,获得利润p是26元(利润=出厂价-成本价),
①求一张薄板的利润p与边长x之间满足的函数关系式.
②当边长为多少时,出厂一张薄板所获得的利润最大?最大利润是多少?
| 薄板的边长x(cm) | 20 | 30 |
| 出厂价y(元/张) | 50 | 70 |
(2)每张薄板的成本价w(单位:元)与它的面积x2(单位:cm2)成正比例,已知出厂一张边长为40cm的薄板,获得利润p是26元(利润=出厂价-成本价),
①求一张薄板的利润p与边长x之间满足的函数关系式.
②当边长为多少时,出厂一张薄板所获得的利润最大?最大利润是多少?
5.观察下列等式:
第一层 1+2=3
第二层 4+5+6=7+8
第三层 9+10+11+12=13+14+15
第四层 16+17+18+19+20=21+22+23+24
…
在上述的数字宝塔中,从上往下数,2017在第( )层.
第一层 1+2=3
第二层 4+5+6=7+8
第三层 9+10+11+12=13+14+15
第四层 16+17+18+19+20=21+22+23+24
…
在上述的数字宝塔中,从上往下数,2017在第( )层.
| A. | 41 | B. | 45 | C. | 43 | D. | 44 |
2.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,先从中摸出一个小球,再从余下的球中摸出一个小球,第二次摸到小球的编号大于第一次编号的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
6.随机掷一枚质地均匀的硬币三次,则至少有一次反面朝上的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{8}$ |
3.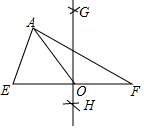 如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
 如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )| A. | AO平分∠EAF | B. | AO垂直平分EF | C. | GH垂直平分EF | D. | GH平分AF |
4.已知一元二次方程x2-2x-1=0的两根分别为x1,x2,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值为( )
| A. | 2 | B. | -1 | C. | $-\frac{1}{2}$ | D. | -2 |
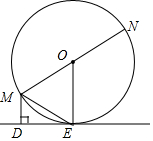 已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.
已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.