题目内容
17.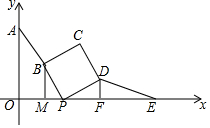 如图,已知A(0,4),E(8,0),点P(a,0)是线段OE上的动点,点B为AP的中点,以BP为边向右边作正方形PBCD,过点B作BM⊥x轴于点M,过点D作DF⊥x轴于点F,连接DE.
如图,已知A(0,4),E(8,0),点P(a,0)是线段OE上的动点,点B为AP的中点,以BP为边向右边作正方形PBCD,过点B作BM⊥x轴于点M,过点D作DF⊥x轴于点F,连接DE.(1)判断DF,BM,MF之间的关系,并说明理由;
(2)求点D的坐标(用含a的代数式表示);
(3)当点P在线段OE(点O,点E除外)上运动时,设△PDE的面积为S,写出S与a的函数关系式,当点P运动到何处时,△PDE的面积最大,最大是多少?
分析 (1)结论:MF=DF+BM.只要证明△PBM≌△DPF,即可推出PM=DF,BM=PF,由此即可解决问题;
(2)利用全等三角形的性质,求出OF、DF的长即可解决问题;
(3)构建二次函数.利用二次函数的性质即可解决问题.
解答 解:(1)结论:MF=DF+BM.
理由:∵四边形ABCD是正方形,
∴PB=PD,∠BPD=90°,
∵BM⊥OE,DF⊥OE,
∴∠BMP=∠DFP=90°,
∵∠BPM+∠DPF=90°,∠MBP+∠BPM=90°,
∴∠MBP=∠DPF,
∴△PBM≌△DPF,
∴PM=DF,BM=PF,
∴MF=MP+PF=DF+BM.
(2)∵A(0,4),P(a,0),
∴OA=4,OP=a,
∵B为AP的中点,
∴B($\frac{a}{2}$,2),BM=PF=2,OM=PM=DF=$\frac{1}{2}$a,
∴D(a+2,$\frac{a}{2}$).
(3)由题意S=$\frac{1}{2}$•PE•DF=$\frac{1}{2}$(8-a)•$\frac{1}{2}$a=$\frac{1}{4}$a(8-a)=-$\frac{1}{4}$(a-4)2+4,
∵-$\frac{1}{4}$<0,
∴a=4时,S有最大值4.
∴当P运动到P(4,0)时,△PDE的面积最大,最大面积为4.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、二次函数的应用等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下列运算结果为a5的是( )
| A. | a2+a3 | B. | a•a5 | C. | (a3)2 | D. | a6÷a |
5.观察下列等式:
第一层 1+2=3
第二层 4+5+6=7+8
第三层 9+10+11+12=13+14+15
第四层 16+17+18+19+20=21+22+23+24
…
在上述的数字宝塔中,从上往下数,2017在第( )层.
第一层 1+2=3
第二层 4+5+6=7+8
第三层 9+10+11+12=13+14+15
第四层 16+17+18+19+20=21+22+23+24
…
在上述的数字宝塔中,从上往下数,2017在第( )层.
| A. | 41 | B. | 45 | C. | 43 | D. | 44 |
2.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,先从中摸出一个小球,再从余下的球中摸出一个小球,第二次摸到小球的编号大于第一次编号的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
6.随机掷一枚质地均匀的硬币三次,则至少有一次反面朝上的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{8}$ |
7.下列方程中,没有实数根的是( )
| A. | x2-2x=0 | B. | x2-2x-1=0 | C. | x2-2x+1=0 | D. | x2-2x+2=0 |