题目内容
7.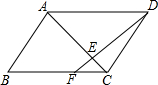 在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 由BC∥AD得$\frac{CE}{AE}=\frac{CF}{AD}$,因为AD=BC,BF=2FC,属于AD=3CF,所以$\frac{CE}{AE}=\frac{1}{3}$,由此可以求出结果.
解答 解: ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴AD∥FC,AD=BC,
∴$\frac{CE}{AE}=\frac{CF}{AD}$,
∵BF=2CF,
∴AD=BC=3FC,
∴$\frac{CE}{AE}=\frac{1}{3}$,
∴$\frac{CE}{CA}=\frac{1}{4}$,
故选C.
点评 本题考查平行四边形的性质、平行线分线段成比例定理等知识,解题的关键是熟练掌握平行线分线段成比例定理,属于中考常考题型.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
17. 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )
 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
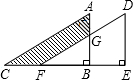 将直角三角形ABC沿CB方向平移BE的距离后,得到直角三角形DEF,已知AG=4,BE=6,DE=12,求阴影部分的面积.
将直角三角形ABC沿CB方向平移BE的距离后,得到直角三角形DEF,已知AG=4,BE=6,DE=12,求阴影部分的面积.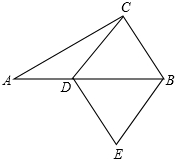 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为AB上一点,以CD,CB边作菱形CDEB,求AD的长.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为AB上一点,以CD,CB边作菱形CDEB,求AD的长.