题目内容
2.计算:(1)(3y-6)(-y);
(2)(-3x)(4x2-$\frac{4}{3}$x+1);
(3)(-xy)(2x-5y-1);
(4)(4y-1)(y-5);
(5)(2x+3)(4x+1);
(6)($\frac{3}{4}$x+1)($\frac{2}{3}$x-3)
分析 (1)(2)(3)根据单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的积相加计算即可;
(4)(5)(6)根据多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn,计算即可.
解答 解:(1)(3y-6)(-y)=-3y2+6y;
(2)(-3x)(4x2-$\frac{4}{3}$x+1)=-12x3+4x2-3x;
(3)(-xy)(2x-5y-1)=-2x2y+5xy2+xy;
(4)(4y-1)(y-5)
=4y2-20y-y+5
=4y2-21y+5;
(5)(2x+3)(4x+1)
=8x2+2x+12x+3
=8x2+14x+3;
(6)($\frac{3}{4}$x+1)($\frac{2}{3}$x-3)
=$\frac{1}{2}$x2-$\frac{9}{4}$x+$\frac{2}{3}$x-3
=$\frac{1}{2}$x2-$\frac{19}{12}$x-3.
点评 考查了单项式与多项式相乘,熟练掌握运算法则是解题的关键,计算时要注意符号的处理.同时考查多项式乘以多项式的法则.注意不要漏项,漏字母,有同类项的合并同类项.

练习册系列答案
相关题目
12.不等式组$\left\{\begin{array}{l}{2(x-1)>x}\\{x≤\frac{x+3}{2}}\end{array}\right.$的解是$\frac{1}{2}$<x≤3.
13.若代数式2a2-a+3的值为5,则代数式4a2-2a+6的值为( )
| A. | -22 | B. | 10 | C. | -10 | D. | 22 |
7.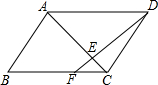 在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
 在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
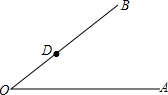 已知,如图,∠A0B边上的点D.过点D作DF∥OA.(保留作图痕迹,不写作法)你有几种方法?
已知,如图,∠A0B边上的点D.过点D作DF∥OA.(保留作图痕迹,不写作法)你有几种方法?