题目内容
15.开学初,小芳和小亮去商店购买学习用品,小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍,已知每支钢笔的价格比每本笔记本的价格少2元.(1)求每支钢笔和每本笔记本各是多少元;
(2)学校运动会后,班主任拿出200元学校奖励基金交给小芳,再次购买上述价格的钢笔和笔记本共48件作为奖品,奖励给校运动会中表现突出的同学,经双方协商,商店给出优惠是购买商品的总金额超出50的部分给打9折,请问小芳至少要买多少支钢笔?
分析 (1)根据小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍,已知每支钢笔的价格比每本笔记本的价铬少2元,可以得到相应的方程,解方程即可求得每支钢笔和每本笔记本各是多少元;
(2)根据题意可以列出相应的不等式,从而可以得到小芳至少要买多少支钢笔.
解答 解:(1)设每本笔记本的价格是x元,则每支钢笔的价格是(x-2)元,
$\frac{30}{x-2}=\frac{25}{x}×2$
解得x=5,
经检验,x=5是原分式方程的解,
则x-2=3,
即每支钢笔和每本笔记本各是3元、5元;
(2)设小芳购买钢笔x支,则购买的笔记本为(48-x)本,
50+[3x+(48-x)×5-50]×0.9≤200
解得x≥11$\frac{2}{3}$,
即小芳至少要买12支钢笔.
点评 本题考查分式方程的应用、一元一次不等式的应用,解题的关键是明确题意,列出相应的分式方程和一元一次不等式,注意分式方程要进行检验.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列变形正确的是( )
| A. | (a2)3=a9 | B. | 2a×3a=6a2 | C. | a6-a2=a4 | D. | 2a+3b=6ab |
20.下列函数的图象中,有最低点的函数是( )
| A. | y=-4x2 | B. | y=-2x+3 | C. | y=3x+5 | D. | y=$\frac{1}{4}$x2 |
7.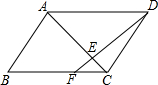 在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
 在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
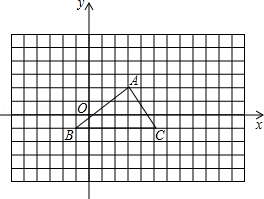 如图所示的网格中,每个小方格都是边长为1的小正方形,B(-1,-1),C(5,-1)
如图所示的网格中,每个小方格都是边长为1的小正方形,B(-1,-1),C(5,-1)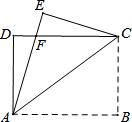 如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=$\frac{25}{4}$,则AD的长为( )
如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=$\frac{25}{4}$,则AD的长为( )