题目内容
12.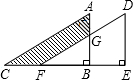 将直角三角形ABC沿CB方向平移BE的距离后,得到直角三角形DEF,已知AG=4,BE=6,DE=12,求阴影部分的面积.
将直角三角形ABC沿CB方向平移BE的距离后,得到直角三角形DEF,已知AG=4,BE=6,DE=12,求阴影部分的面积.
分析 根据平移的性质可得AB=DE=12,S△ABC=S△DEF,从而可得S阴影=S四边形DEBG,只需求出梯形DEBG的面积,就可解决问题.
解答 解:由平移可得:AB=DE=12,S△ABC=S△DEF,
∴BG=AB-AG=12-4=8,S阴影=S四边形DEBG
=$\frac{1}{2}$(12+8)×6=60.
点评 本题主要考查了平移的性质、等式的性质、梯形的面积等知识,将阴影部分的面积转化为梯形DEBG的面积,是解决本题的关键.

练习册系列答案
相关题目
20.下列函数的图象中,有最低点的函数是( )
| A. | y=-4x2 | B. | y=-2x+3 | C. | y=3x+5 | D. | y=$\frac{1}{4}$x2 |
7.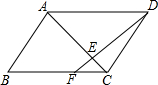 在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
 在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
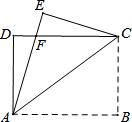 如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=$\frac{25}{4}$,则AD的长为( )
如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=$\frac{25}{4}$,则AD的长为( )