题目内容
17.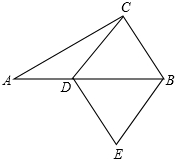 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为AB上一点,以CD,CB边作菱形CDEB,求AD的长.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为AB上一点,以CD,CB边作菱形CDEB,求AD的长.
分析 首先在Rt△ABC中利用勾股定理求出AB=5,再连接CE交AB于点H,根据△ABC的面积表达式求出CH,继而利用勾股定理求出BH,从而可求AD.
解答 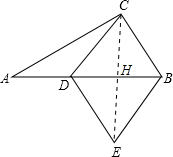 解:∵在Rt△ABC中,∠ACB=90°,AC=4,BC=3,
解:∵在Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5.
连接CE交AB于点H,
在菱形CDEB中,CE⊥BD且HD=HB,CD=CB,
∵S△ABC=$\frac{1}{2}$AB×CH=$\frac{1}{2}$AC×BC,
∴CH=$\frac{AC×BC}{AB}$=$\frac{12}{5}$,
在Rt△BCH中,HB=$\sqrt{B{C}^{2}-C{H}^{2}}$=$\frac{9}{5}$,
∴AD=AB-2BH=5-2×$\frac{9}{5}$=$\frac{7}{5}$.
点评 本题考查了菱形的性质、勾股定理及三角形的面积,解答本题的关键是正确求出CH的长.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
7.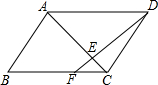 在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
 在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
19.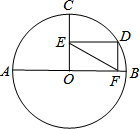 如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
 如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )| A. | OE•OF≤1 | B. | OE•OF≤2 | C. | OE•OF≤3 | D. | OE•OF≤4 |