题目内容
16.如果一个自然数能表示为两个自然数的平方差,那么称这个自然数为智慧数,例如:16=52-32,16就是一个智慧数,小明和小王对自然数中的智慧数迸行了如下的探索:小明的方法是一个一个找出来的:
0=02-02,1=12-02,3=22-12,
4=22-02,5=32-22,7=42-32,
8=32-12,9=52-42,11=62-52,…
小王认为小明的方法太麻烦,他想到:
设k是自然数,由于(k+1)2-k2=(k+1+k)(k+1-k)=2k+1.
所以,自然中所有奇数都是智慧数.
问题:(1)根据上述方法,自然数中第12个智慧数是15.
(2)他们发现0,4,8是智慧数,由此猜测4k(k≥3且k为正整数)都是智慧数,请你参考小王的办法证明4k(k≥3且k为正整数)都是智慧数.
(3)他们还发现2,6,10都不是智慧数,由此猜测4k+2(k为自然数)都不是智慧数,请利用所学的知识判断26是否是智慧数,并说明理由.
分析 (1)仿照小明的办法,继续下去,即可得出结论;
(2)仿照小王的做法,将(k+2)2-k2用平方差公式展开即可得出结论;
(3)验证26是否符合4k+2,如果符合,则得出26不是智慧数.
解答 (1)解:继续小明的方法,12=42-22,13=72-62,15=82-72,
即第12个智慧数是15.
故答案为:15.
(2)证明:设k是自然数,由于(k+2)2-k2=(k+2+k)(k+2-k)=4k+4=4(k+1).
所以,4k(k≥3且k为正整数)都是智慧数.
(3)解:令4k+2=26,解得:k=6.
故26不是智慧数.
点评 本题考查了新定义智慧数以及平方差公式的运用,解题的关键是:(1)仿照小明的办法继续找下去;(2)将将(k+2)2-k2用平方差公式展开;(3)令4k+2=26,求出k值.本题属于基础题,难度不大,题中文字较多,很多学生不喜欢这样的文字题,解决该类型题时,只要仿照文中给定的办法即可得出结论.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
7.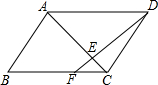 在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
 在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )
在?ABCD中,点F时BC边上一点,且BF=2CF,DF交对角线AC于点E,则$\frac{CE}{AC}$等于( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
19.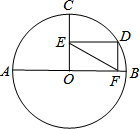 如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
 如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )| A. | OE•OF≤1 | B. | OE•OF≤2 | C. | OE•OF≤3 | D. | OE•OF≤4 |
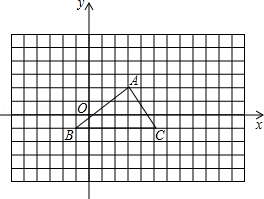 如图所示的网格中,每个小方格都是边长为1的小正方形,B(-1,-1),C(5,-1)
如图所示的网格中,每个小方格都是边长为1的小正方形,B(-1,-1),C(5,-1)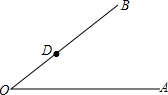 已知,如图,∠A0B边上的点D.过点D作DF∥OA.(保留作图痕迹,不写作法)你有几种方法?
已知,如图,∠A0B边上的点D.过点D作DF∥OA.(保留作图痕迹,不写作法)你有几种方法?