题目内容
一个两位数,个位上数字是a,十位上数字是b.若一个两位数等于各位数字之和的4倍,则称这个两位数为“巧数”.请写出所有的“巧数”,并说明理由.
考点:二元一次方程的应用
专题:数字问题
分析:首先根据题意可得到方程:10b+a=4(b+a),化简得a=2b,又由a,b是不为0的一位数,分析得到这样的“巧数”有4个,写出即可.
解答:解:依题意有10b+a=4(b+a),
即a=2b,
∵a,b是不为0的一位数,
∴b<5,
∴当b=1时,a=2,则此两位数为12;
当b=2时,a=4,则此两位数为24;
当b=3时,a=6,则此两位数为36;
当b=4时,a=8,则此两位数为48.
故所有的“巧数”是12,24,36,48.
即a=2b,
∵a,b是不为0的一位数,
∴b<5,
∴当b=1时,a=2,则此两位数为12;
当b=2时,a=4,则此两位数为24;
当b=3时,a=6,则此两位数为36;
当b=4时,a=8,则此两位数为48.
故所有的“巧数”是12,24,36,48.
点评:此题考查了二元一次方程的应用,数字的表示方法与性质.注意根据题意求得方程,利用方程思想求解是解此题的关键.

练习册系列答案
相关题目
 如图点C是线段BD上一点,分别以BC和CD为一边,在BD的同侧作等边△ABC和等边△ECD,AC交BE于点G,CE交AD于点F.
如图点C是线段BD上一点,分别以BC和CD为一边,在BD的同侧作等边△ABC和等边△ECD,AC交BE于点G,CE交AD于点F. 如图所示,在正方形ABCD中,E是正方形边AD上一点,F是BA延长线上一点,并且AF=AE.
如图所示,在正方形ABCD中,E是正方形边AD上一点,F是BA延长线上一点,并且AF=AE. 如图,已知CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且OB=OC.
如图,已知CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且OB=OC.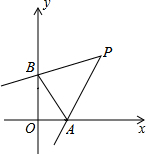 如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是
如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是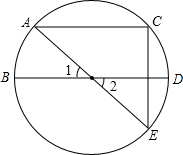 如图,直径AE,BD交于点O,点D为
如图,直径AE,BD交于点O,点D为