题目内容
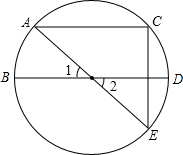 如图,直径AE,BD交于点O,点D为
如图,直径AE,BD交于点O,点D为 |
| CE |
 |
| AB |
 |
| CE |
考点:圆心角、弧、弦的关系
专题:证明题
分析:先根据点D为
中点得出BD⊥CE,
=2
,再由圆周角定理得出∠C=90°,故AC⊥CE,所以AC∥BD,故
=
,由此可得出结论.
 |
| CE |
 |
| CE |
 |
| CD |
 |
| AB |
 |
| CD |
解答:证明:∵点D为
中点,
∴BD⊥CE,
=2
.
∵AE是⊙O的直径,
∴∠C=90°,
∴AC⊥CE,
∴AC∥BD,
∴
=
,
∴2
=
.
 |
| CE |
∴BD⊥CE,
 |
| CE |
 |
| CD |
∵AE是⊙O的直径,
∴∠C=90°,
∴AC⊥CE,
∴AC∥BD,
∴
 |
| AB |
 |
| CD |
∴2
 |
| AB |
 |
| CE |
点评:本题考查的是圆心角、弧、弦的关系,熟知在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若
=
,则
的值等于( )
| a |
| b |
| 4 |
| 3 |
| a+b |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
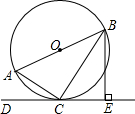 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线DC⊥BE于点E,BC平分∠ABE,连接AC.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线DC⊥BE于点E,BC平分∠ABE,连接AC. 如图,⊙O是△ABC的外接圆,AB是直径,OD∥AC,且∠CBD=∠BAC,OD交⊙O于点E,交BC于F.
如图,⊙O是△ABC的外接圆,AB是直径,OD∥AC,且∠CBD=∠BAC,OD交⊙O于点E,交BC于F. 在Rt△ABC中,∠C=90°,c=3,∠A=30°,求b和a的值.
在Rt△ABC中,∠C=90°,c=3,∠A=30°,求b和a的值.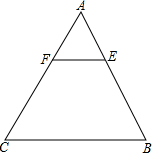 如图,在△ABC中,AE:EB=1;2,EF∥BC,求S△AEF:S△ABC的值.
如图,在△ABC中,AE:EB=1;2,EF∥BC,求S△AEF:S△ABC的值.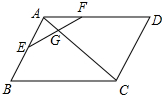 如图,在平行四边形ABCD中,E、F分别在AB、AD上,EF交AC于点G,若AE:EB=2:3,AF:FD=3:2,则AG:AC等于多少?
如图,在平行四边形ABCD中,E、F分别在AB、AD上,EF交AC于点G,若AE:EB=2:3,AF:FD=3:2,则AG:AC等于多少?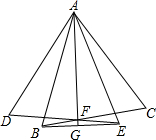 如图,等边△ABC绕点A顺时针旋转到△ADE,BC与DE相交于点F,连接AF并延长,交BE于点G,求证:AF⊥BE.
如图,等边△ABC绕点A顺时针旋转到△ADE,BC与DE相交于点F,连接AF并延长,交BE于点G,求证:AF⊥BE.