题目内容
 如图,已知CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且OB=OC.
如图,已知CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且OB=OC.求证:AO平分∠BAC.
考点:全等三角形的判定与性质
专题:证明题
分析:先证明△BOD≌△COE,得出OD=OE,证出点O在∠BAC的平分线上,即可证出AO平分∠BAC.
解答:证明:∵CD⊥AB,BE⊥AC,
∴∠BDO=∠CEO=90°,
在△BOD和△COE中,
∴△BOD≌△COE(AAS),
∴OD=OE,
∴点O在∠BAC的平分线上,
即AO平分∠BAC.
∴∠BDO=∠CEO=90°,
在△BOD和△COE中,
|
∴△BOD≌△COE(AAS),
∴OD=OE,
∴点O在∠BAC的平分线上,
即AO平分∠BAC.
点评:本题考查了全等三角形的判定与性质以及角的平分线的判定;证明三角形全等是解决问题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
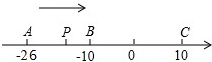 如图,已知数轴上有A、B、C三点,分别表示有理数-26、-10、10,动点P从点A出发,以每秒1个单位的速度向终点C移动,当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,问当点Q从A点出发几秒钟时,点P和点Q相距2个单位长度?直接写出此时点Q在数轴上表示的有理数.
如图,已知数轴上有A、B、C三点,分别表示有理数-26、-10、10,动点P从点A出发,以每秒1个单位的速度向终点C移动,当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,问当点Q从A点出发几秒钟时,点P和点Q相距2个单位长度?直接写出此时点Q在数轴上表示的有理数.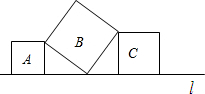 如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为
如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为
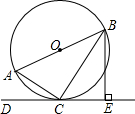 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线DC⊥BE于点E,BC平分∠ABE,连接AC.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线DC⊥BE于点E,BC平分∠ABE,连接AC.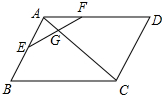 如图,在平行四边形ABCD中,E、F分别在AB、AD上,EF交AC于点G,若AE:EB=2:3,AF:FD=3:2,则AG:AC等于多少?
如图,在平行四边形ABCD中,E、F分别在AB、AD上,EF交AC于点G,若AE:EB=2:3,AF:FD=3:2,则AG:AC等于多少?