题目内容
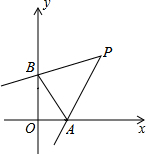 如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是
如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:连接OP,作PF⊥y轴,PE⊥x轴.在x轴上截取ED=OF=OE=2,再截取DC=OB,可以证明△PBA≌△PCA,由此可得出结论.
解答: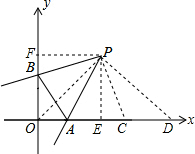 解:连接OP,作PF⊥y轴,PE⊥x轴,在x轴上截取ED=OF=OE=2,再截取DC=OB.
解:连接OP,作PF⊥y轴,PE⊥x轴,在x轴上截取ED=OF=OE=2,再截取DC=OB.
∵点P(2,2),
∴PA=PB=BD=OA=OB=2,
∴OD=4,∠PDC=∠FOP=∠POA=45°.
在△PBO与△PCD中,
,
∴△PBO≌△PCD(SAS).
∴PC=PB.
在△PFB与△PEC中,
,
∴△PFB≌△PEC(SAS),
∴∠FPB=∠EPC.
又∵∠APB=45°,
∴∠FPB+∠EPC=45°,
∴∠CPA=∠EPC+∠APE=∠FPB+∠APE=∠BPA=45°.
在△PBA与△PCA中,
,
∴△PBA≌△PCA(SAS),
∴△OAB的周长=OB+OA+AB=CD+OA+CE=OD=4.
故答案为:4.
 解:连接OP,作PF⊥y轴,PE⊥x轴,在x轴上截取ED=OF=OE=2,再截取DC=OB.
解:连接OP,作PF⊥y轴,PE⊥x轴,在x轴上截取ED=OF=OE=2,再截取DC=OB.∵点P(2,2),
∴PA=PB=BD=OA=OB=2,
∴OD=4,∠PDC=∠FOP=∠POA=45°.
在△PBO与△PCD中,
|
∴△PBO≌△PCD(SAS).
∴PC=PB.
在△PFB与△PEC中,
|
∴△PFB≌△PEC(SAS),
∴∠FPB=∠EPC.
又∵∠APB=45°,
∴∠FPB+∠EPC=45°,
∴∠CPA=∠EPC+∠APE=∠FPB+∠APE=∠BPA=45°.
在△PBA与△PCA中,
|
∴△PBA≌△PCA(SAS),
∴△OAB的周长=OB+OA+AB=CD+OA+CE=OD=4.
故答案为:4.
点评:本题考查的是全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
下列叙述正确的是( )
| A、“13位同学中有两人出生的月份相同”是随机事件 |
| B、小亮掷硬币100次,其中44次正面朝上,则小亮掷硬币一次正面朝上的概率为0.44 |
| C、“明天降雨的概率是80%”,即明天下雨有80%的可能性 |
| D、彩票的中奖概率为1%,买100张才会中奖 |

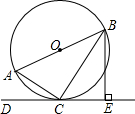 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线DC⊥BE于点E,BC平分∠ABE,连接AC.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线DC⊥BE于点E,BC平分∠ABE,连接AC. 如图,⊙O是△ABC的外接圆,AB是直径,OD∥AC,且∠CBD=∠BAC,OD交⊙O于点E,交BC于F.
如图,⊙O是△ABC的外接圆,AB是直径,OD∥AC,且∠CBD=∠BAC,OD交⊙O于点E,交BC于F.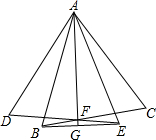 如图,等边△ABC绕点A顺时针旋转到△ADE,BC与DE相交于点F,连接AF并延长,交BE于点G,求证:AF⊥BE.
如图,等边△ABC绕点A顺时针旋转到△ADE,BC与DE相交于点F,连接AF并延长,交BE于点G,求证:AF⊥BE.