题目内容
已知三项式mx2+5xy-2y2有一个因式是3x-y，求m的值并将这个二次三项式分解因式．
考点：因式分解的应用
专题：
分析：设另一个因式是（bx+2y），则（3x-y）（bx+2y）=3bx2+（6-b）xy-2y2，根据对应项的系数相等即可求得b和m的值．
解答：解：设另一个因式是（bx+2y），
则（3x-y）（bx+2y）=3bx2+（6-b）xy-2y2=mx2+5xy-2y2，
6-b=5，m=3b，
因此b=1，m=3．
3x2+5xy-2y2=（3x-y）（x+2y）．
则（3x-y）（bx+2y）=3bx2+（6-b）xy-2y2=mx2+5xy-2y2，
6-b=5，m=3b，
因此b=1，m=3．
3x2+5xy-2y2=（3x-y）（x+2y）．
点评：本题考查了因式分解的意义，正确理解因式分解与整式的乘法互为逆运算是关键．
练习册系列答案
相关题目
如图，要测量河两岸相对的两点A、B间的距离，先在过点B的AB的垂线l上取两点C、D，使CD=BC，再在过D的垂线上取点E，使A、C、E在一条直线上，这时△ACB≌△ECD，DE=AB．测得DE的长就是A、B的距离，这里判断△ACB≌△ECD的理由是（ ）| A、SAS | B、ASA |
| C、AAS | D、SSS |
已知a+b=4n+2，ab=1．若19a2+147ab+19b2的值为2845，则n的值为（ ）
| A、±2.5 |
| B、1.5或2.5 |
| C、2.5或-3.5 |
| D、±3.5 |
一双运动鞋先按成本提高40%标价，再以8折（标价的80%）出售，结果获利27元，若设这双运动鞋的成本价是x元，根据题意，可得到的方程是（ ）
| A、（1+40%）x•80%=x-27 |
| B、（1+40%）x•80%=x+27 |
| C、（1-40%）x•80%=x+27 |
| D、（1-40%）x•80%=x+27 |
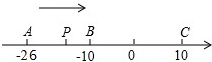如图，已知数轴上有A、B、C三点，分别表示有理数-26、-10、10，动点P从点A出发，以每秒1个单位的速度向终点C移动，当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，问当点Q从A点出发几秒钟时，点P和点Q相距2个单位长度？直接写出此时点Q在数轴上表示的有理数．