题目内容
 如图所示,在正方形ABCD中,E是正方形边AD上一点,F是BA延长线上一点,并且AF=AE.
如图所示,在正方形ABCD中,E是正方形边AD上一点,F是BA延长线上一点,并且AF=AE.(1)求证:△ABE≌△ADF;
(2)指出图中线段BE与DF之间数量和位置的关系,并加以证明.
考点:全等三角形的判定与性质,正方形的性质
专题:
分析:(1)根据正方形的性质得出AD=AB,∠FAD=∠EAB=90°,根据SAS即可推出答案.
(2)延长BE交DF于G,根据全等三角形的性质得BE=DF,∠ABE=∠ADF,得到∠ABE+∠AEB=∠ADF+∠DEG=90°,即BE⊥DF.所以BE=DF且BE⊥DF.
(2)延长BE交DF于G,根据全等三角形的性质得BE=DF,∠ABE=∠ADF,得到∠ABE+∠AEB=∠ADF+∠DEG=90°,即BE⊥DF.所以BE=DF且BE⊥DF.
解答:证明:(1)∵四边形ABCD是正方形,
∴AD=AB,∠FAD=∠EAB=90°,
在△ABE与△ADF中,
,
∴△ABE≌△ADF(SAS).
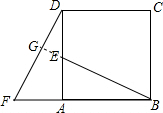
(2)延长BE交DF于G,如图,
∵△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠AEB=∠DEG,∠BAE=90°
∴∠ABE+∠AEB=∠ADF+∠DEG=90°,
∴∠DGE=90°,
即BE⊥DF.
故BE=DF且BE⊥DF.
∴AD=AB,∠FAD=∠EAB=90°,
在△ABE与△ADF中,
|
∴△ABE≌△ADF(SAS).

(2)延长BE交DF于G,如图,
∵△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠AEB=∠DEG,∠BAE=90°
∴∠ABE+∠AEB=∠ADF+∠DEG=90°,
∴∠DGE=90°,
即BE⊥DF.
故BE=DF且BE⊥DF.
点评:本题主要考查对正方形的性质,全等三角形的判定和性质等知识点的理解和掌握,能正确运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
一双运动鞋先按成本提高40%标价,再以8折(标价的80%)出售,结果获利27元,若设这双运动鞋的成本价是x元,根据题意,可得到的方程是( )
| A、(1+40%)x•80%=x-27 |
| B、(1+40%)x•80%=x+27 |
| C、(1-40%)x•80%=x+27 |
| D、(1-40%)x•80%=x+27 |
下列事件中,必然事件是( )
| A、抛掷1个均匀的骰子,出现6点向上 |
| B、两直线被第三条直线所截,同位角相等 |
| C、366人中至少有2人的生日相同 |
| D、实数的绝对值是非负数 |
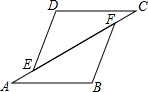 已知:如图,点E、F在线段AC上,AB∥CD,AE=CF,
已知:如图,点E、F在线段AC上,AB∥CD,AE=CF,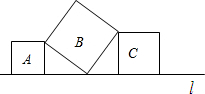 如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为
如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为
 在Rt△ABC中,∠C=90°,c=3,∠A=30°,求b和a的值.
在Rt△ABC中,∠C=90°,c=3,∠A=30°,求b和a的值.