题目内容
2．用反证法证明“a≤b“时，应假设（ ）| A． | a＞b | B． | a＜b | C． | a=b | D． | a≥b |
分析 反证法的步骤中，第一步是假设结论不成立，反面成立．
解答 解：用反证法证明“a≤b”时，应先假设a＞b．
故选：A．
点评 此题考查了反证法，解此题关键要懂得反证法的意义及步骤．在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．
练习册系列答案
相关题目
13．下列图形中，是中心对称图形但不是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
10．下列计算正确的是（ ）
| A． | $\sqrt{3}$×$\sqrt{2}$=2$\sqrt{3}$ | B． | $\sqrt{6}$÷$\sqrt{2}$=$\sqrt{3}$ | C． | $\sqrt{6}$+$\sqrt{2}$=$\sqrt{8}$ | D． | $\sqrt{6}$-$\sqrt{2}$=$\sqrt{4}$ |
17．如果下列各组数是三角形的三边长，那么能组成直角三角形的是（ ）
| A． | 2，3，4 | B． | 3，4，5 | C． | 4，5，6 | D． | 5，6，7 |
7．下列算式正确的是（ ）
| A． | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | B． | $\sqrt{2}$÷$\sqrt{3}$=$\sqrt{5}$ | C． | 5$\sqrt{5}$-2$\sqrt{2}$=3$\sqrt{3}$ | D． | $\sqrt{2}$÷$\sqrt{3}$=$\frac{\sqrt{6}}{3}$ |
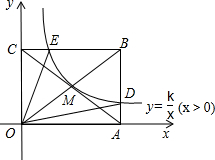如图，反比例函数y=$\frac{k}{x}$（x＞0）的图象经过矩形OABC对角线的交点M，分别与AB，BC交于点D，E，若四边形ODBE的面积为6，则△OAD的面积为（ ）
【合作学习】如图，矩形ABOD的两边OB，OD都在坐标轴的正半轴上，OD=3，另两边与反比例函数y=$\frac{k}{x}$（k≠0）的图象分别相交于点E，F，且DE=2．过点E作EH⊥x轴于点H，过点F作FG⊥EH于点G．回答下面的问题：