题目内容
 如图,已知Rt△ABC中,∠C=90°.
如图,已知Rt△ABC中,∠C=90°.(1)作∠BAC的角平分线AD交BC边于D,以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹)
(2)设(1)中⊙O的半径为r,若AB=4,∠B=30°,求r的值.
考点:作图—复杂作图
专题:
分析:(1)作出∠BAC的角平分线进而得出进而作线段AD的垂直平分线得出即可;
(2)根据锐角三角函数关系得出CD的长,再利用30°所对的边是斜边的一半,得出AD以及EO的长即可.
(2)根据锐角三角函数关系得出CD的长,再利用30°所对的边是斜边的一半,得出AD以及EO的长即可.
解答: 解:(1)如图所示:
解:(1)如图所示:
(2)作AD的垂直平分线交AB于点O,交AD于点E,
∵∠C=90°,∠B=30°,
∴∠1=∠2=30°,
由AB=4,知AC=2,
∴tan30°=
,
∴CD=
,AD=
,
易知AE=
,则EO=AEtan30°=
,故AO=
,
即:r=
.
 解:(1)如图所示:
解:(1)如图所示:(2)作AD的垂直平分线交AB于点O,交AD于点E,
∵∠C=90°,∠B=30°,
∴∠1=∠2=30°,
由AB=4,知AC=2,
∴tan30°=
| CD |
| AC |
∴CD=
2
| ||
| 3 |
4
| ||
| 3 |
易知AE=
2
| ||
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
即:r=
| 4 |
| 3 |
点评:此题主要考查了角平分线的性质与作法以及锐角三角函数关系等知识,得出AD的长是解题关键.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 如图,O是平行四边形ABCD对角线BD的中点,过点O作一直线EF交CD于点E,交AB于点F,设四边形AFED与四边形FBCE的面积分别为S1,S2,则S1与S2的大小关系是( )
如图,O是平行四边形ABCD对角线BD的中点,过点O作一直线EF交CD于点E,交AB于点F,设四边形AFED与四边形FBCE的面积分别为S1,S2,则S1与S2的大小关系是( )| A、S1>S2 |
| B、S1<S2 |
| C、S1=S2 |
| D、不能确定 |
以方程组
的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
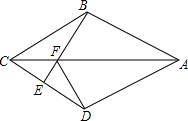 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,连结BE交AC于点F,连结DF.
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,连结BE交AC于点F,连结DF.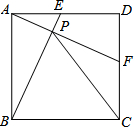 如图,正方形ABCD中,点E从点A出发沿着AD向D运动,(点E不与点A,点D重合)同时点F从点D出发沿着线段DC向C运动,(点F不与点D,点C重合)点E与F点运动速度相同,当点E停止运动时,另一动点F随之停止运动,设BE与AF相交于点P,连接PC请研究:
如图,正方形ABCD中,点E从点A出发沿着AD向D运动,(点E不与点A,点D重合)同时点F从点D出发沿着线段DC向C运动,(点F不与点D,点C重合)点E与F点运动速度相同,当点E停止运动时,另一动点F随之停止运动,设BE与AF相交于点P,连接PC请研究: