题目内容
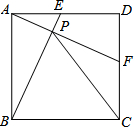 如图,正方形ABCD中,点E从点A出发沿着AD向D运动,(点E不与点A,点D重合)同时点F从点D出发沿着线段DC向C运动,(点F不与点D,点C重合)点E与F点运动速度相同,当点E停止运动时,另一动点F随之停止运动,设BE与AF相交于点P,连接PC请研究:
如图,正方形ABCD中,点E从点A出发沿着AD向D运动,(点E不与点A,点D重合)同时点F从点D出发沿着线段DC向C运动,(点F不与点D,点C重合)点E与F点运动速度相同,当点E停止运动时,另一动点F随之停止运动,设BE与AF相交于点P,连接PC请研究:(1)AF=BE,AF⊥BE;
(2)当点E运动到AD中点位置时:
①PA:PB的值是多少?②PC和BC又怎样的数量关系?并证明你的结论.
考点:正方形的性质,全等三角形的判定与性质
专题:动点型
分析:(1)根据题意很容易证得△BAE≌△ADF,即可得到AF=BE,利用正方形内角为90°,得出AF⊥DE.
(2)要求两条线段的关系,需要把两者放入一直角三角形中,利用三角函数求解.根据题意可知此时AF⊥BE,又有中点的关系,可以得出tan∠2=
,由∠1=∠2,可以求解.
(3)延长AF交BC的延长线于点G,可以得出△ADF≌△GCF,进而得出CG=AD,通过线段的转换可以得出BC=
BG,根据题意可以得出PC=
BG,即可以得出结论.
(2)要求两条线段的关系,需要把两者放入一直角三角形中,利用三角函数求解.根据题意可知此时AF⊥BE,又有中点的关系,可以得出tan∠2=
| 1 |
| 2 |
(3)延长AF交BC的延长线于点G,可以得出△ADF≌△GCF,进而得出CG=AD,通过线段的转换可以得出BC=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:∵E在AD边上(不与A、D重合),点F在DC边上(不与D、C重合).
又∵点E、F分别同时从A、D出发以相同的速度运动,
∴AE=DF,
∵四边形ABCD是正方形,
∴AB=DA,∠BAE=∠D=90°,
在△BAE和△ADF中,
,
∴△BAE≌△ADF(SAS),
∴∠1=∠2,
∵∠2+∠3=90°∴∠1+∠3=90°即∠APB=90°
∴AF⊥BE.
(2)解:由(1)知当点E运动到AD中点时,点F也运动到DC中点,此时就有AF⊥BE.
∵F是CD的中点,
∴DF=
CD,
∵AD=CD,
∴DF=
AD,
∵∠1=∠2,
∴tan∠1=tan∠2
在Rt△ADF中,tan∠2=
=
,
∴在Rt△APB中,tan∠1=
∴PA:PB的值是1:2.
(3)PC=BC.
证明:延长AF交BC的延长线于点G,
在△ADF和△GCF中
,
∴△ADF≌△GCF(ASA),
∴CG=AD,
∵BC=AD,
∴CG=BC=
BG,
由(1)知AF⊥BE,
∴∠BPG=90°,
∴△BPG为直角三角形
∴PC=
BG,
∵BC=
BG,
∴PC=BC.
又∵点E、F分别同时从A、D出发以相同的速度运动,
∴AE=DF,
∵四边形ABCD是正方形,
∴AB=DA,∠BAE=∠D=90°,
在△BAE和△ADF中,
|
∴△BAE≌△ADF(SAS),
∴∠1=∠2,
∵∠2+∠3=90°∴∠1+∠3=90°即∠APB=90°
∴AF⊥BE.
(2)解:由(1)知当点E运动到AD中点时,点F也运动到DC中点,此时就有AF⊥BE.
∵F是CD的中点,
∴DF=
| 1 |
| 2 |
∵AD=CD,
∴DF=
| 1 |
| 2 |
∵∠1=∠2,
∴tan∠1=tan∠2
在Rt△ADF中,tan∠2=
| DF |
| AD |
| 1 |
| 2 |
∴在Rt△APB中,tan∠1=
∴PA:PB的值是1:2.

(3)PC=BC.
证明:延长AF交BC的延长线于点G,
在△ADF和△GCF中
|
∴△ADF≌△GCF(ASA),
∴CG=AD,
∵BC=AD,
∴CG=BC=
| 1 |
| 2 |
由(1)知AF⊥BE,
∴∠BPG=90°,
∴△BPG为直角三角形
∴PC=
| 1 |
| 2 |
∵BC=
| 1 |
| 2 |
∴PC=BC.
点评:本题考查了正方形的性质以及全等三角形的判定和性质,对学生要求有比较高的读图能力,同时本题也是探求性试题,做这类题前要求大胆的假设,根据假设再去证明.需要在平时做题中培养这种能力.

练习册系列答案
相关题目
 如图,已知Rt△ABC中,∠C=90°.
如图,已知Rt△ABC中,∠C=90°. 如图,已知△ABC内部有一点O,连结BO、CO,D、G、E、F分别是AB、AC、BO、CO的中点,连结DG、GF、EF、DE.
如图,已知△ABC内部有一点O,连结BO、CO,D、G、E、F分别是AB、AC、BO、CO的中点,连结DG、GF、EF、DE.