题目内容
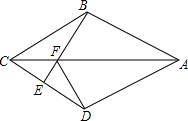 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,连结BE交AC于点F,连结DF.
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,连结BE交AC于点F,连结DF.(1)证明:△ABF≌△ADF;
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,又知∠EFD=∠BCD,请问你能推出什么结论?(直接写出一个结论,要求结论中含有字母E)
考点:菱形的判定,全等三角形的判定与性质
专题:
分析:(1)首先证明△ABC≌△ADC得出∠1=∠2,进而求出利用已知求出△ABF≌△ADF;
(2)利用AB∥CD,则∠1=∠3,进而得出AD=CD,即可求出AB=CB=CD=AD求出即可;
(3)利用(2)中所求可得出∠CBE=∠CDF,则可得出BE⊥CD或∠BEC=∠BED=90°或△BEC∽△DEF或∠EFD=∠BAD等.
(2)利用AB∥CD,则∠1=∠3,进而得出AD=CD,即可求出AB=CB=CD=AD求出即可;
(3)利用(2)中所求可得出∠CBE=∠CDF,则可得出BE⊥CD或∠BEC=∠BED=90°或△BEC∽△DEF或∠EFD=∠BAD等.
解答: (1)证明:
(1)证明:
在△ABC和△ADC中
∴△ABC≌△ADC(SSS),
∴∠1=∠2,
在△ABF和△ADF中
∴△ABF≌△ADF(SAS)
(2)证明:∵AB∥CD,∴∠1=∠3,
又∵∠1=∠2,∴∠2=∠3,∴AD=CD,
∵AB=AD,CB=CD,∴AB=CB=CD=AD,
∴四边形ABCD是菱形;
(3)由(2)可得:BE⊥CD或∠BEC=∠BED=90°或△BEC∽△DEF或∠EFD=∠BAD,写出其中一个.
 (1)证明:
(1)证明:在△ABC和△ADC中
|
∴△ABC≌△ADC(SSS),
∴∠1=∠2,
在△ABF和△ADF中
|
∴△ABF≌△ADF(SAS)
(2)证明:∵AB∥CD,∴∠1=∠3,
又∵∠1=∠2,∴∠2=∠3,∴AD=CD,
∵AB=AD,CB=CD,∴AB=CB=CD=AD,
∴四边形ABCD是菱形;
(3)由(2)可得:BE⊥CD或∠BEC=∠BED=90°或△BEC∽△DEF或∠EFD=∠BAD,写出其中一个.
点评:此题主要考查了菱形的判定与性质以及全等三角形的判定与性质等知识,得出△ABC≌△ADC是解题关键.

练习册系列答案
相关题目
一元二次方程x2=-(
+1)x-2的根的情况是( )
| 3 |
| A、有两个相等的实数根 |
| B、没有实数根 |
| C、有两个不相等的实数根 |
| D、无法确定 |
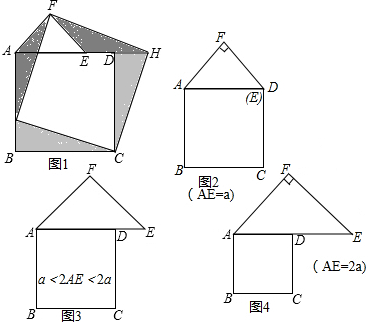
 如图,已知Rt△ABC中,∠C=90°.
如图,已知Rt△ABC中,∠C=90°. 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.