题目内容
15.点P(-2,b)是反比例函数y=$\frac{2}{x}$的图象上的一点,则b=( )| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
分析 直接将点P(-2,b)代入y=$\frac{2}{x}$即可求出b的值.
解答 解:∵点P(-2,b)是反比例函数y=$\frac{2}{x}$的图象上的一点,
∴-2b=2,
解得:b=-1,
故选B.
点评 题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数.

练习册系列答案
相关题目
5.计算:$\sqrt{3}×\sqrt{6}$的结果是( )
| A. | $9\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{6}$ |
6.从2,-2,1,-1四个数中任取2个不同的数求和,其和为1的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
10.某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
现要配制这种营养食品20千克,要求每千克至少含有9600单位的维生素C.设购买甲种原料x千克.
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?最少费用是多少?
| 原料 维生素C及价格 | 甲种原料 | 乙种原料 |
| 维生素C(单位/千克) | 600 | 400 |
| 原料价格(元/千克) | 9 | 5 |
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?最少费用是多少?
5.已知a,b,c为△ABC三边,且满足(a2-b2)(a2+b2-c2)=0,则它的形状为( )
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰三角形或直角三角形 |
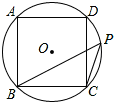 如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠BPC的度数是45°.
如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠BPC的度数是45°.