题目内容
5．已知a，b，c为△ABC三边，且满足（a2-b2）（a2+b2-c2）=0，则它的形状为（ ）| A． | 直角三角形 | B． | 等腰三角形 | ||
| C． | 等腰直角三角形 | D． | 等腰三角形或直角三角形 |
分析 首先根据题意可得（a2-b2）（a2+b2-c2）=0，进而得到a2+b2=c2，或a=b，根据勾股定理逆定理可得△ABC的形状为等腰三角形或直角三角形．
解答 解：（a2-b2）（a2+b2-c2）=0，
∴a2+b2-c2，或a-b=0，
解得：a2+b2=c2，或a=b，
∴△ABC的形状为等腰三角形或直角三角形．
故选D．
点评 此题主要考查了勾股定理逆定理以及非负数的性质，关键是掌握勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．
练习册系列答案
备战中考寒假系列答案
相关题目
15．点P（-2，b）是反比例函数y=$\frac{2}{x}$的图象上的一点，则b=（ ）
| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
20．数据：2，-1，3，5，6，5的众数是（ ）
| A． | -1 | B． | 4 | C． | 5 | D． | 6 |
17．在函数y=$\frac{{-{k^2}-1}}{x}$（k为常数）的图象上有三个点（x1，-2），（x2，-1），（x3，3），则x1，x2，x3的大小关系为（ ）
| A． | x1＜x2＜x3 | B． | x3＜x1＜x2 | C． | x3＜x2＜x1 | D． | x2＜x1＜x3 |
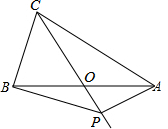如图，在△ABC中，AB=AC=4，AO=BO，P是射线CO上的一个动点，∠AOC=120°，则当△PAB为直角三角形时，AP的长为2或2$\sqrt{3}$．
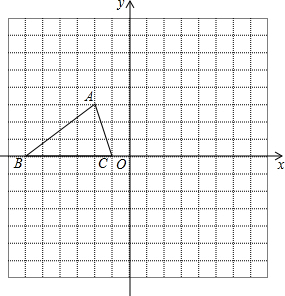△ABC在平面直角坐标系中的位置如图所示，A、B、C三点在格点上：