题目内容
7．
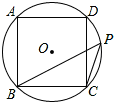如图，正方形ABCD的四个顶点分别在⊙O上，点P在$\widehat{CD}$上不同于点C的任意一点，则∠BPC的度数是45°．
分析 连接OB，OC，先根据正方形的性质求出∠BOC的度数，再由圆周角定理即可得出结论．
解答 
解：连接OB，OC，
∵四边形ABCD是正方形，
∴∠BOC=$\frac{1}{4}$×360°=90°，
∴∠BPC=$\frac{1}{2}$∠BOC=45°．
故答案为：45°．
点评 本题考查的是圆周角定理，根据题意作出辅助线，构造出圆心角是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．点P（-2，b）是反比例函数y=$\frac{2}{x}$的图象上的一点，则b=（ ）
| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
2．下列不是二次函数关系的是（ ）
| A． | y=3x2+4 | B． | y=2x2-x-1 | C． | $y=\frac{8}{x}$ | D． | y=x（x+1） |
17．在函数y=$\frac{{-{k^2}-1}}{x}$（k为常数）的图象上有三个点（x1，-2），（x2，-1），（x3，3），则x1，x2，x3的大小关系为（ ）
| A． | x1＜x2＜x3 | B． | x3＜x1＜x2 | C． | x3＜x2＜x1 | D． | x2＜x1＜x3 |