题目内容
6.从2,-2,1,-1四个数中任取2个不同的数求和,其和为1的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 列举出所有情况,让和为1的情况数除以总情况数即为所求的概率.
解答 解:列表得:
| 2 | -2 | 1 | -1 | |
| 2 | 4 | 0 | 3 | 1 |
| -2 | 0 | -4 | -1 | -3 |
| 1 | 3 | -1 | 2 | 0 |
| -1 | 1 | -3 | 0 | -2 |
∴和为1的概率=$\frac{2}{12}$=$\frac{1}{6}$,
故选A.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
11.化简(a-1)•$\sqrt{\frac{1}{1-a}}$的结果是( )
| A. | -$\sqrt{1-a}$ | B. | $\sqrt{1-a}$ | C. | -$\sqrt{a-1}$ | D. | $\sqrt{a-1}$ |
15.点P(-2,b)是反比例函数y=$\frac{2}{x}$的图象上的一点,则b=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
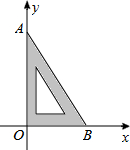 如图,把含有30°角的三角板ABO置入平面直角坐标系中,AB=4,则点A的坐标为(0,2$\sqrt{3}$).
如图,把含有30°角的三角板ABO置入平面直角坐标系中,AB=4,则点A的坐标为(0,2$\sqrt{3}$).