题目内容
11.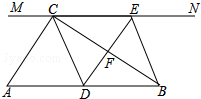 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB中点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB中点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.(1)若∠A=60°,AB=10,求四边形ABEC的周长;
(2)当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
分析 (1)只要证明四边形ACED是平行四边形,四边形BDCE是菱形即可解决问题;
(2)当∠A=45°,四边形BECD是正方形.只要证明∠CEB=90°即可;
解答 (1)解:∵∠ACB=90°,DE⊥BC,
∴∠DFB=∠ACB=90°,
∴AC∥DE,
∵CE∥AD,
∴四边形ACED是平行四边形,
AD=EC=DB,∵CE∥DB,
∴四边形BDCE是平行四边形,
∵CD=DA=DB,
∴四边形BDCE是菱形,
在Rt△ACB中,∵∠ACB=90°,∠A=60°,AB=10,
∴AC=$\frac{1}{2}$AB=5,
∴CE=EB=BD=AD=5,
∴四边形ABEC的周长为25.
(2)结论:当∠A=45°,四边形BECD是正方形.
理由:∵四边形ACED是平行四边形,
∴∠A=∠CED=45°,
∵四边形BDCE是菱形,
∴∠CED=∠DEB=45°,
∴∠CEB=90°,
∴四边形BDCE是正方形.
点评 本题考查平行四边形的判定和性质、菱形的判定和性质、正方形的判定、直角三角形30度角性质等知识,解题的关键是熟练掌握基本知识,灵活应用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
1. 直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )
直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )
 直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )
直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )| A. | 30° | B. | 36° | C. | 45° | D. | 72° |
1.有五张不透明的卡片,正面的数分别写有3.101001000,$\frac{7}{3}$,π,$\sqrt{6}$,3.$\stackrel{••}{12}$,除正面的数不同外,其余都相同,将它们背面朝上洗匀后,从中随机抽取一张卡片,抽到写有有理数卡片的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图:∠A=40°,∠B=24°,把△ABC绕点C按顺时针方向旋转到△AB′C′,使点B′在AC的延长线上,则△ABC旋转了64度.
如图:∠A=40°,∠B=24°,把△ABC绕点C按顺时针方向旋转到△AB′C′,使点B′在AC的延长线上,则△ABC旋转了64度.