题目内容
3.计算与求值.已知a=$\frac{1}{{2+\sqrt{3}}}$,求$\frac{{a}^{2}-2a+1}{a-1}$-$\frac{\sqrt{{a}^{2}-2a+1}}{{a}^{2}-a}$的值.
分析 首先关键a的值求得$\frac{1}{a}$=2+$\sqrt{3}$,a-1=1-$\sqrt{3}$<0,然后把原代数式变形为a-1+$\frac{1}{a}$,再进一步代入求得数值即可.
解答 解:∵a=$\frac{1}{{2+\sqrt{3}}}$,
∴a=2-$\sqrt{3}$,
∴$\frac{1}{a}$=2+$\sqrt{3}$,a-1=1-$\sqrt{3}$<0,
∴$\frac{{a}^{2}-2a+1}{a-1}$-$\frac{\sqrt{{a}^{2}-2a+1}}{{a}^{2}-a}$
=$\frac{(a-1)^{2}}{a-1}$+$\frac{a-1}{a(a-1)}$
=a-1+$\frac{1}{a}$
=1-$\sqrt{3}$+2+$\sqrt{3}$
=3.
点评 此题考查二次根式的化简求值,利用完全平方公式把代数式变形,问题简单易懂.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
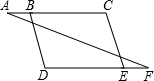 完成下面的证明(在括号中填写推理理由)
完成下面的证明(在括号中填写推理理由)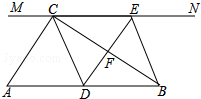 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB中点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB中点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE. 如图是小芹3月1日-7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是1.5小时.
如图是小芹3月1日-7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是1.5小时.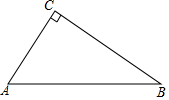 如图,已知△CAB,∠ACB=90°.
如图,已知△CAB,∠ACB=90°.