题目内容
1．有五张不透明的卡片，正面的数分别写有3.101001000，$\frac{7}{3}$，π，$\sqrt{6}$，3.$\stackrel{••}{12}$，除正面的数不同外，其余都相同，将它们背面朝上洗匀后，从中随机抽取一张卡片，抽到写有有理数卡片的概率为（ ）| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
分析 用有理数卡片的数量除以卡片的总数量，据此可得．
解答 解：在正面的数分别写有3.101001000，$\frac{7}{3}$，π，$\sqrt{6}$，3.$\stackrel{••}{12}$的5张卡片中，有理数的有3.101001000、$\frac{7}{3}$、3.$\stackrel{••}{12}$这3张，
∴从中随机抽取一张卡片，抽到写有有理数卡片的概率为$\frac{3}{5}$，
故选：C．
点评 题考查的是概率的求法．如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=$\frac{m}{n}$．
练习册系列答案
相关题目
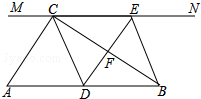如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D在AB中点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．
9．在平面直角坐标系中，下列坐标所对应的点位于第三象限的是（ ）
| A． | （-1，-3） | B． | （-3，0） | C． | （1，-4） | D． | （3，2） |
将一副直角三角尺如图放置（其中∠A=60°，∠F=45°），点E在AC上，ED∥BC，则∠AEF的度数是165°．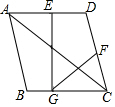
已知：如图，平行四边形ABCD中，点E，F分别是AD，CD的中点，EG⊥BC，垂足为点G，连接FG，求证：AC=2GF．
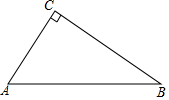如图，已知△CAB，∠ACB=90°．