题目内容
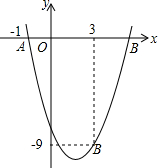 如图,二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).
如图,二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).(1)求该二次函数的解析式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)若点P与点Q均是该函数图象上的点,且这两点关于抛物线的对称轴对称,点P到x轴的距离为6,求点P与点Q的距离PQ.
考点:待定系数法求二次函数解析式,二次函数的性质,二次函数图象上点的坐标特征
专题:
分析:(1)将点A(-1,-1)和点B(3,-9)分别代入y=ax2-4x+c求解即可,
(2)由二次函数顶点式可得答案,
(3)令x2-4x-6=6或-6分别求出x的值,即可求出PQ的值.
(2)由二次函数顶点式可得答案,
(3)令x2-4x-6=6或-6分别求出x的值,即可求出PQ的值.
解答:解:(1)将点A(-1,-1)和点B(3,-9)分别代入y=ax2-4x+c,
得
,
解得
,
∴二次函数的表达式为y=x2-4x-6.
(2)∵二次函数的表达式为y=x2-4x-6=(x-2)2-10,
∴对称轴为直线x=2;顶点坐标为(2,-10).
(3)令x2-4x-6=6,解得,x1=-2,x2=6.
令x2-4x-6=-6 解得,x1=0,x2=4.
∴PQ=8或4.
得
|
解得
|
∴二次函数的表达式为y=x2-4x-6.
(2)∵二次函数的表达式为y=x2-4x-6=(x-2)2-10,
∴对称轴为直线x=2;顶点坐标为(2,-10).
(3)令x2-4x-6=6,解得,x1=-2,x2=6.
令x2-4x-6=-6 解得,x1=0,x2=4.
∴PQ=8或4.
点评:本题主要考查了待定系数法求二次函数及二次函数的性质,解题的关键是正确求出二次函数的正确表达式.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
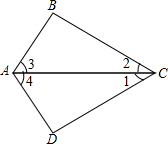 如图,AC是△ABC和△ADC的公共边,要判定△ABC≌△ADC还需要补充的条件不能是( )
如图,AC是△ABC和△ADC的公共边,要判定△ABC≌△ADC还需要补充的条件不能是( )| A、AB=AD,∠1=∠2 |
| B、AB=AD,∠3=∠4 |
| C、∠1=∠2,∠3=∠4 |
| D、∠1=∠2,∠B=∠D |
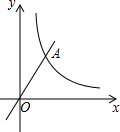 已知图中的曲线是反比例函数y=
已知图中的曲线是反比例函数y=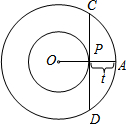 如图,已知OA=4cm,一个动点P从A向O以1cm/秒的速度运动,以O为圆心,分别以OA、OP为半径画大圆和小圆,以P为切点的小圆的切线与大圆交于C、D,则弦CD的长y(cm)关于P的运动时间t(秒)的函数解析式为
如图,已知OA=4cm,一个动点P从A向O以1cm/秒的速度运动,以O为圆心,分别以OA、OP为半径画大圆和小圆,以P为切点的小圆的切线与大圆交于C、D,则弦CD的长y(cm)关于P的运动时间t(秒)的函数解析式为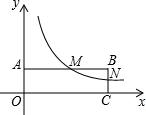 如图,在平面直角坐标系中,点A和点C分别在y轴和x轴的正半轴上,以OA、OC为边作矩形OABC,双曲线
如图,在平面直角坐标系中,点A和点C分别在y轴和x轴的正半轴上,以OA、OC为边作矩形OABC,双曲线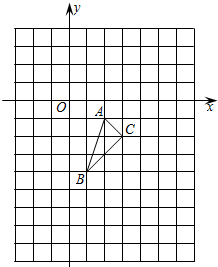 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-1)、B(1,-4)、C(3,-2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-1)、B(1,-4)、C(3,-2).