题目内容
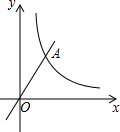 已知图中的曲线是反比例函数y=
已知图中的曲线是反比例函数y=| m-5 |
| x |
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)由反比例函数图象位于第一象限得到m-5大于0,即可求出m的范围;
(2)将A坐标代入正比例函数解析式中求出n的值,确定出A坐标,代入反比例解析式中求出m的值,即可确定出反比例解析式;
(2)将A坐标代入正比例函数解析式中求出n的值,确定出A坐标,代入反比例解析式中求出m的值,即可确定出反比例解析式;
解答:解:(1)∵这个反比例函数的图象分布在第一、第三象限,
∴m-5>0,
解得m>5.
(2)∵点A (2,n)在正比例函数y=2x的图象上,
∴n=2×2=4,
则A点的坐标为(2,4).
∴m-5>0,
解得m>5.
(2)∵点A (2,n)在正比例函数y=2x的图象上,
∴n=2×2=4,
则A点的坐标为(2,4).
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:反比例函数的图象与性质,一次函数图象上点的坐标特征.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 如图所示,在Rt△ABC中,∠C=90°,∠B=2∠A,AB=6cm,则BC的长是( )
如图所示,在Rt△ABC中,∠C=90°,∠B=2∠A,AB=6cm,则BC的长是( )| A、2cm | B、4cm |
| C、6cm | D、3cm |
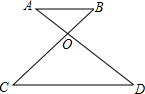 如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )
如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )| A、BO:BC=1:2 |
| B、CD:AB=2:1 |
| C、CO:BC=1:2 |
| D、AD:DO=3:1 |
 有理数a、b在数轴上的位置如图所示,在下列结论中:
有理数a、b在数轴上的位置如图所示,在下列结论中:①ab<0;②a+b>0;③a3>b2;④(a-b)3<0;⑤a<-b<b<-a;⑥|b-a|-|a|=b.其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
一个圆锥的冰淇淋纸筒,其底面直径为6cm,母线长为5cm,围成这样的冰淇淋纸筒所需纸片的面积为( )
| A、15πcm2 |
| B、30πcm2 |
| C、18πcm2 |
| D、12πcm2 |
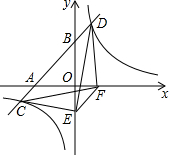 如图,一次函数y=x+3的图象与x轴,y轴交于A、B两点,与反比例函数y=
如图,一次函数y=x+3的图象与x轴,y轴交于A、B两点,与反比例函数y=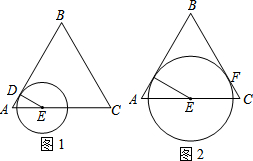 己知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒,
己知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒,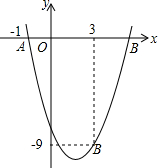 如图,二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).
如图,二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).