题目内容
已知|x-12|+|z-13|与y2-24y+144互为相反数,则以x、y、z为三边的三角形是 三角形.
考点:等腰三角形的判定,非负数的性质:绝对值,非负数的性质:偶次方,配方法的应用
专题:常规题型
分析:根据相反数的意义得到|x-12|+|z-13|+y2-24y+144=0,配方得|x-12|+|z-13|+(y-12)2=0,则根据非负数的性质得到x-12=0,z-13=0,y-12=0,解方程可得到x=y,然后根据等腰三角形的判定定理得到以x、y、z为三边的三角形是等腰三角形.
解答:解:∵|x-12|+|z-13|与y2-24y+144互为相反数,
∴|x-12|+|z-13|+y2-24y+144=0,
即|x-12|+|z-13|+(y-12)2=0,
∴x-12=0,z-13=0,y-12=0,解得x=12,z=13,y=12,
∴x=y,
∴以x、y、z为三边的三角形是等腰三角形.
故答案为等腰.
∴|x-12|+|z-13|+y2-24y+144=0,
即|x-12|+|z-13|+(y-12)2=0,
∴x-12=0,z-13=0,y-12=0,解得x=12,z=13,y=12,
∴x=y,
∴以x、y、z为三边的三角形是等腰三角形.
故答案为等腰.
点评:本题考查了等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等.也考查了配方法和非负数的性质.

练习册系列答案
相关题目
 如图所示,在Rt△ABC中,∠C=90°,∠B=2∠A,AB=6cm,则BC的长是( )
如图所示,在Rt△ABC中,∠C=90°,∠B=2∠A,AB=6cm,则BC的长是( )| A、2cm | B、4cm |
| C、6cm | D、3cm |
△ABC中,AB=AC,AB边的中垂线与直线AC所成的角为50°,则∠B等于( )
| A、70° |
| B、20°或70° |
| C、40°或70° |
| D、40°或20° |
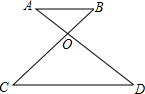 如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )
如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )| A、BO:BC=1:2 |
| B、CD:AB=2:1 |
| C、CO:BC=1:2 |
| D、AD:DO=3:1 |
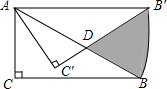 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是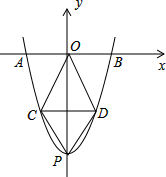 已知抛物线y=x2-8与x轴相交于两点A,B,与y轴相交于点P,
已知抛物线y=x2-8与x轴相交于两点A,B,与y轴相交于点P,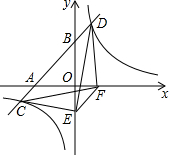 如图,一次函数y=x+3的图象与x轴,y轴交于A、B两点,与反比例函数y=
如图,一次函数y=x+3的图象与x轴,y轴交于A、B两点,与反比例函数y=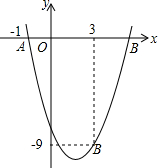 如图,二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).
如图,二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).