题目内容
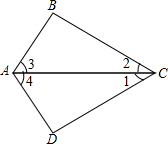 如图,AC是△ABC和△ADC的公共边,要判定△ABC≌△ADC还需要补充的条件不能是( )
如图,AC是△ABC和△ADC的公共边,要判定△ABC≌△ADC还需要补充的条件不能是( )| A、AB=AD,∠1=∠2 |
| B、AB=AD,∠3=∠4 |
| C、∠1=∠2,∠3=∠4 |
| D、∠1=∠2,∠B=∠D |
考点:全等三角形的判定
专题:
分析:对所给的条件逐一判断、分析,即可解决问题.
解答: 解:要判定△ABC≌△ADC,
解:要判定△ABC≌△ADC,
还需要补充的条件不能是A.理由如下:
若A成立,则在△ABC与△ADC中,
∵AB=AD,∠1=∠2,AC=AC,
即两个三角形中,满足有两边及其中一边所对的角相等,
∴这两个三角形不一定全等,
故选A.
 解:要判定△ABC≌△ADC,
解:要判定△ABC≌△ADC,还需要补充的条件不能是A.理由如下:
若A成立,则在△ABC与△ADC中,
∵AB=AD,∠1=∠2,AC=AC,
即两个三角形中,满足有两边及其中一边所对的角相等,
∴这两个三角形不一定全等,
故选A.
点评:该题考查了判断两个三角形全等的条件及其应用问题;解题的关键是牢固掌握全等三角形的判定定理.

练习册系列答案
相关题目
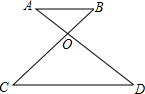 如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )
如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )| A、BO:BC=1:2 |
| B、CD:AB=2:1 |
| C、CO:BC=1:2 |
| D、AD:DO=3:1 |
 有理数a、b在数轴上的位置如图所示,在下列结论中:
有理数a、b在数轴上的位置如图所示,在下列结论中:①ab<0;②a+b>0;③a3>b2;④(a-b)3<0;⑤a<-b<b<-a;⑥|b-a|-|a|=b.其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
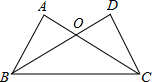 如图,AC与DB相交于点O,已知∠ABC=∠DCB,图中再补充一个条件后可证明△ABC≌△DCB,则这个条件不能是( )
如图,AC与DB相交于点O,已知∠ABC=∠DCB,图中再补充一个条件后可证明△ABC≌△DCB,则这个条件不能是( )| A、AB=DC |
| B、∠A=∠D |
| C、OB=OC |
| D、AC=DB |
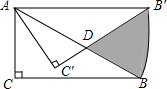 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是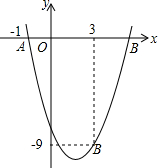 如图,二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).
如图,二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).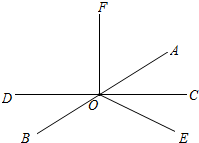 如图,已知过点O的直线AB平分∠EOF,∠COF=90°,∠EOF=116°.求:
如图,已知过点O的直线AB平分∠EOF,∠COF=90°,∠EOF=116°.求: