题目内容
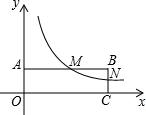 如图,在平面直角坐标系中,点A和点C分别在y轴和x轴的正半轴上,以OA、OC为边作矩形OABC,双曲线y=
如图,在平面直角坐标系中,点A和点C分别在y轴和x轴的正半轴上,以OA、OC为边作矩形OABC,双曲线y=| 2 |
| x |
考点:反比例函数图象上点的坐标特征
专题:
分析:根据反比例函数图象上点的坐标特征,利用AM=BM=2,求得M点横坐标,代入y=
(x>0)即可求得M的坐标,从而求得B的坐标.
| 2 |
| x |
解答:解:∵AM=BM=2,
∴M点横坐标为2,AB=4,
∵M在双曲线y=
(x>0)上,
∴M(2,1),
∴B(4,1).
故答案为:(4,1).
∴M点横坐标为2,AB=4,
∵M在双曲线y=
| 2 |
| x |
∴M(2,1),
∴B(4,1).
故答案为:(4,1).
点评:本题考查了反比例函数图象上点的坐标特征以及矩形的性质.

练习册系列答案
相关题目
 有理数a、b在数轴上的位置如图所示,在下列结论中:
有理数a、b在数轴上的位置如图所示,在下列结论中:①ab<0;②a+b>0;③a3>b2;④(a-b)3<0;⑤a<-b<b<-a;⑥|b-a|-|a|=b.其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
一个圆锥的冰淇淋纸筒,其底面直径为6cm,母线长为5cm,围成这样的冰淇淋纸筒所需纸片的面积为( )
| A、15πcm2 |
| B、30πcm2 |
| C、18πcm2 |
| D、12πcm2 |
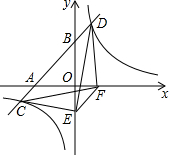 如图,一次函数y=x+3的图象与x轴,y轴交于A、B两点,与反比例函数y=
如图,一次函数y=x+3的图象与x轴,y轴交于A、B两点,与反比例函数y=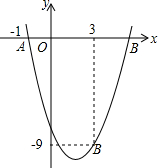 如图,二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).
如图,二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).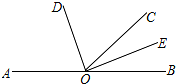 如图,点A、O、B在同一条直线上,射线OD与射线OE分别平分∠AOC和∠BOC
如图,点A、O、B在同一条直线上,射线OD与射线OE分别平分∠AOC和∠BOC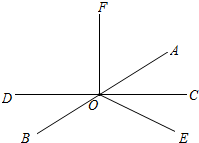 如图,已知过点O的直线AB平分∠EOF,∠COF=90°,∠EOF=116°.求:
如图,已知过点O的直线AB平分∠EOF,∠COF=90°,∠EOF=116°.求: