题目内容
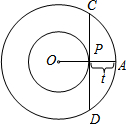如图，已知OA=4cm，一个动点P从A向O以1cm/秒的速度运动，以O为圆心，分别以OA、OP为半径画大圆和小圆，以P为切点的小圆的切线与大圆交于C、D，则弦CD的长y（cm）关于P的运动时间t（秒）的函数解析式为考点：切线的性质,勾股定理,垂径定理
专题：
分析：根据切线的性质求得OP⊥CD，根据垂径定理求得CD=2PC=2PD，根据已知求得OP=（4-t）cm，然后根据勾股定理即可求得解析式．
解答：
解：∵P为切点的小圆的切线与大圆交于C、D，
∴OP⊥CD，
∴CD=2PC=2PD，
连接OC，
∵OA=4cm，
∴OP=（4-t）cm，
在RT△POC中，PC=
=
=
，
∴y=2
，（0≤t≤4）
故答案为：y=2
，（0≤t≤4）．
解：∵P为切点的小圆的切线与大圆交于C、D，∴OP⊥CD，
∴CD=2PC=2PD，
连接OC，
∵OA=4cm，
∴OP=（4-t）cm，
在RT△POC中，PC=
| OC2-OP2 |
| 42-(4-t)2 |
| 8t-t2 |
∴y=2
| 8t-t2 |
故答案为：y=2
| 8t-t2 |
点评：本题考查了切线的性质，垂径定理以及勾股定理的应用，作出辅助线根据直角三角形是关键．
练习册系列答案
习题精选系列答案
相关题目
△ABC中，AB=AC，AB边的中垂线与直线AC所成的角为50°，则∠B等于（ ）
| A、70° |
| B、20°或70° |
| C、40°或70° |
| D、40°或20° |
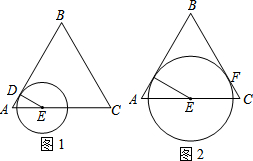己知等边△ABC，边长为4，点D从点A出发，沿AB运动到点B，到点B停止运动．点E从A出发，沿AC的方向在直线AC上运动．点D的速度为每秒1个单位，点E的速度为每秒2个单位，它们同时出发，同时停止．以点E为圆心，DE长为半径作圆．设E点的运动时间为t秒，
有理数a、b在数轴上的位置如图所示，在下列结论中：
如图，已知AB=DB，要使△ABC≌△DBC，还要添加什么条件？添加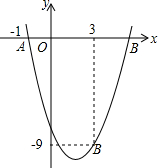
如图，二次函数y=ax2-4x+c的图象经过点A（-1，-1）和点B（3，-9）．
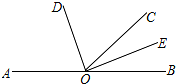如图，点A、O、B在同一条直线上，射线OD与射线OE分别平分∠AOC和∠BOC