题目内容
20．
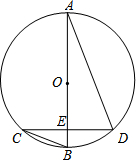如图，AB是⊙O的直径，且点B是$\widehat{CD}$的中点，AB交CD于E，若∠C=21°，则∠ADC=69°．
分析 先根据圆周角定理求出∠A的度数，再由点B是$\widehat{CD}$的中点可得出$\widehat{BC}$的度数，进可得出$\widehat{AC}$的度数，由圆心角、弧、弦的关系即可得出结论．
解答 解：∵∠C=21°，
∴∠A=∠C=21°．
∵点B是$\widehat{CD}$的中点，
∴$\widehat{BC}$的度数为42°．
∵AB是⊙O的直径，
∴$\widehat{AC}$的度数=180°-42°=138°，
∴∠ADC=$\frac{1}{2}$×138°=69°．
故答案为：69°．
点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在平行四边形ABCD中，EF∥AB交AD于E交BD于F，DE：EA=3：4，EF=6，则CD的长为14．
15．
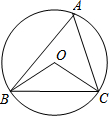如图，⊙O的半径为2，△ABC是⊙O的内接三角形，连结OB，OC，若∠BAC与∠BOC互补，则弦BC的长为（ ）
如图，⊙O的半径为2，△ABC是⊙O的内接三角形，连结OB，OC，若∠BAC与∠BOC互补，则弦BC的长为（ ）| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 2$\sqrt{2}$ | D． | 4 |
5．下列各式的值一定是正数的是（ ）
| A． | |a| | B． | $\sqrt{a^2}$ | C． | $\frac{1}{a^2}$ | D． | $\root{3}{a}$ |
如图放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为1的等边三角形，点A在x轴上，点O，B1，B2，B3，…都在直线l上，则点A2的坐标是（2，$\sqrt{3}$），点A2017的坐标是（$\frac{2019}{2}$，$\frac{2017\sqrt{3}}{2}$）．
9．
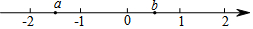实数a，b在数轴上的位置如图所示，以下说法正确的是（ ）
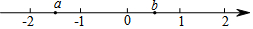实数a，b在数轴上的位置如图所示，以下说法正确的是（ ）| A． | a+b＞0 | B． | a-b＞0 | C． | $\frac{a}{b}$＞0 | D． | b2＜a2 |
10．矩形ABCD的边AB=3 cm，AD=4 cm，以A为圆心，4 cm为半径作⊙A，则点C与⊙A的位置关系为（ ）
| A． | 点C在⊙A内 | B． | 点C不一定在⊙A外 | C． | 点C在⊙A上 | D． | 点C在⊙A外 |