题目内容
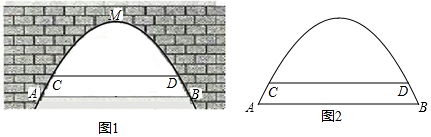
11.如图1.抛物线y=-x2+bx+c经过点A(-3.0),点C(0,3).点D为抛物线的顶点.抛物线的对称轴DE交x轴于点E.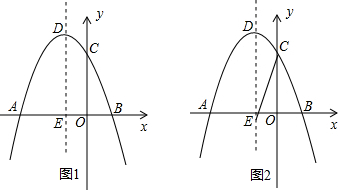
(1 )求抛物线的解析式.
(2)在DE上求点P到AD的距离与到x轴的距离相等.
(3)如图2.在DE的左侧抛物线上求点F,使S△FBC=$\frac{3}{2}$S△EBC.
分析 (1)把A、C两点坐标代入可求得b、c,可求得抛物线解析式;
(2)当点P在∠DAB的平分线上时,过P作PM⊥AD,设出P点坐标,可表示出PM、PE,由角平分线的性质可得到PM=PE,可求得P点坐标;当点P在∠DAB外角平分线上时,同理可求得P点坐标;
(3)可先求得△FBC的面积,过F作FQ⊥x轴,交BC的延长线于Q,可求得FQ的长,可设出F点坐标,表示出B点坐标,从而可表示出FQ的长,可求得F点坐标.
解答 解:(1)∵二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),
∴$\left\{\begin{array}{l}{c=3}\\{-9-3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式y=-x2-2x+3;
(2)当P在∠DAB的平分线上时,如图1,作PM⊥AD,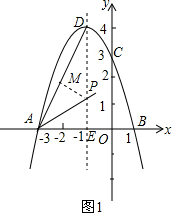
设P(-1,m),则PM=PD•sin∠ADE=$\frac{\sqrt{5}}{5}$(4-m),PE=m,
∵PM=PE,
∴$\frac{\sqrt{5}}{5}$(4-m)=m,m=$\sqrt{5}$-1,
∴P点坐标为(-1,$\sqrt{5}$-1);
当P在∠DAB的外角平分线上时,如图2,作PN⊥AD,
设P(-1,n),则PN=PD•sin∠ADE=$\frac{\sqrt{5}}{5}$(4-n),PE=-n,
∵PN=PE,
∴$\frac{\sqrt{5}}{5}$(4-n)=-n,n=-$\sqrt{5}$-1,
∴P点坐标为(-1,-$\sqrt{5}$-1);
综上可知存在满足条件的P点,其坐标为(-1,$\sqrt{5}$-1)或(-1,-$\sqrt{5}$-1);
(3)∵抛物线的解析式y=-x2-2x+3,
∴B(1,0),
∴S△EBC=$\frac{1}{2}$EB•OC=3,
∵2S△FBC=3S△EBC,
∴S△FBC=$\frac{9}{2}$,
过F作FQ⊥x轴于点H,交BC的延长线于Q,过F作FM⊥y轴于点M,如图3,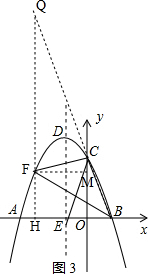
∵S△FBC=S△BQH-S△BFH-S△CFQ
=$\frac{1}{2}$HB•HQ-$\frac{1}{2}$BH•HF-$\frac{1}{2}$QF•FM
=$\frac{1}{2}$BH(HQ-HF)-$\frac{1}{2}$QF•FM
=$\frac{1}{2}$BH•QF-$\frac{1}{2}$QF•FM
=$\frac{1}{2}$QF•(BH-FM)
=$\frac{1}{2}$FQ•OB
=$\frac{1}{2}$FQ
=$\frac{9}{2}$,
∴FQ=9,
∵BC的解析式为y=-3x+3,
设F(x0,-x02-2x0+3),
∴-3x0+3+x02+2x0-3=9,
解得:x0=$\frac{1-\sqrt{37}}{2}$或$\frac{1+\sqrt{37}}{2}$(舍去),
∴点F的坐标是($\frac{1-\sqrt{37}}{2}$,$\frac{3\sqrt{37}-15}{2}$),
∵S△ABC=6>$\frac{9}{2}$,
∴点F不可能在A点下方,
综上可知F点的坐标为($\frac{1-\sqrt{37}}{2}$,$\frac{3\sqrt{37}-15}{2}$).
点评 本题主要考查二次函数的综合应用,涉及待定系数法、角平分线的性质、三角函数、三角形面积等知识点.在(1)中注意待定系数法的应用步骤,在(2)中注意分点P在∠DAB的角平分线上和在外角的平分线上两种情况,在(3)中求得FQ的长是解题的关键.

 阅读快车系列答案
阅读快车系列答案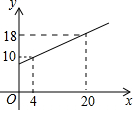 若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数图象如图,则不挂重物时,弹簧的长度是( )
若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数图象如图,则不挂重物时,弹簧的长度是( )| A. | 5cm | B. | 8cm | C. | 9cm | D. | 10cm |
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
| A. | 2x-1 | B. | 2x+1 | C. | $\frac{1}{2}({x-1})$ | D. | $\frac{1}{2}({x+1})$ |
 如图,?ABCD中,AB>BC,∠BAD与∠ADC的平分线交于点E,∠ABC与∠BCD的平分线交于点F.
如图,?ABCD中,AB>BC,∠BAD与∠ADC的平分线交于点E,∠ABC与∠BCD的平分线交于点F.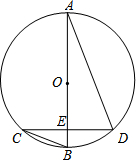 如图,AB是⊙O的直径,且点B是$\widehat{CD}$的中点,AB交CD于E,若∠C=21°,则∠ADC=69°.
如图,AB是⊙O的直径,且点B是$\widehat{CD}$的中点,AB交CD于E,若∠C=21°,则∠ADC=69°.