题目内容
10．请先化简（$\frac{2x}{x-3}$-$\frac{x}{x+3}$）÷$\frac{x}{{x}^{2}-9}$，再选取一个既使原式有意义，又是你喜欢的数代入求值．分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．
解答 解：原式=$\frac{2x（x+3）-x（x-3）}{（x+3）（x-3）}$•$\frac{（x+3）（x-3）}{x}$=$\frac{x[2（x+3）-（x-3）]}{x}$=2（x+3）-（x-3）=2x+6-x+3=x+9，
当x=1时，原式=1+9=10．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
1．
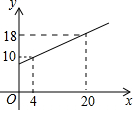若弹簧的总长度y（cm）是所挂重物x（千克）的一次函数图象如图，则不挂重物时，弹簧的长度是（ ）
若弹簧的总长度y（cm）是所挂重物x（千克）的一次函数图象如图，则不挂重物时，弹簧的长度是（ ）| A． | 5cm | B． | 8cm | C． | 9cm | D． | 10cm |
5．独山县各学校开展了第二课堂的活动，在某校国学诗词组、篮球足球组、陶艺茶艺组三个活动组织中，若小斌和小宇两名同学每人随机选择其中一个活动参加，则小斌和小宇选到同一活动的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{9}$ |
15．点P（3，5）关于原点中心对称的点的坐标是（ ）
| A． | （5，3） | B． | （-3，5） | C． | （3，-5） | D． | （-3，-5） |
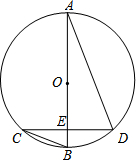如图，AB是⊙O的直径，且点B是$\widehat{CD}$的中点，AB交CD于E，若∠C=21°，则∠ADC=69°．