题目内容
15.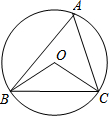 如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 4 |
分析 作弦心距OD,先根据已知求出∠BOC=120°,由等腰三角形三线合一的性质得:∠DOC=$\frac{1}{2}$∠BOC=60°,利用30°角所对的直角边是斜边的一半可求得OD的长,根据勾股定理得DC的长,最后利用垂径定理得出结论.
解答 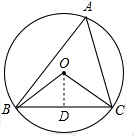 解∵∠BAC与∠BOC互补,
解∵∠BAC与∠BOC互补,
∴∠BAC+∠BOC=180°,
∵∠BAC=$\frac{1}{2}$∠BOC,
∴∠BOC=120°,
过O作OD⊥BC,垂足为D,
∴BD=CD,
∵OB=OC,
∴OB平分∠BOC,
∴∠DOC=$\frac{1}{2}$∠BOC=60°,
∴∠OCD=90°-60°=30°,
在Rt△DOC中,OC=2,
∴OD=1,
∴DC=$\sqrt{3}$,
∴BC=2DC=2$\sqrt{3}$,
故选B.
点评 本题考查了圆周角定理、垂径定理及等腰三角形三线合一的性质,熟练掌握垂径定理是关键,本题中利用圆周角定理中圆周角与圆心角的关系得出角的度数,从而得到△ODC是30°的直角三角形,根据30°角所对的直角边是斜边的一半得到OD的长,从而得出弦BC的长.

练习册系列答案
相关题目
5.独山县各学校开展了第二课堂的活动,在某校国学诗词组、篮球足球组、陶艺茶艺组三个活动组织中,若小斌和小宇两名同学每人随机选择其中一个活动参加,则小斌和小宇选到同一活动的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
 如图,?ABCD中,AB>BC,∠BAD与∠ADC的平分线交于点E,∠ABC与∠BCD的平分线交于点F.
如图,?ABCD中,AB>BC,∠BAD与∠ADC的平分线交于点E,∠ABC与∠BCD的平分线交于点F. 已知,如图,AC⊥BC,BD⊥BC,AC>BC>BD.
已知,如图,AC⊥BC,BD⊥BC,AC>BC>BD.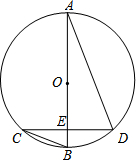 如图,AB是⊙O的直径,且点B是$\widehat{CD}$的中点,AB交CD于E,若∠C=21°,则∠ADC=69°.
如图,AB是⊙O的直径,且点B是$\widehat{CD}$的中点,AB交CD于E,若∠C=21°,则∠ADC=69°.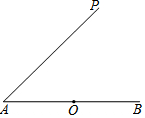 如图,已知O是∠PAB的一边AB上的点,按要求作图:
如图,已知O是∠PAB的一边AB上的点,按要求作图: 如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为30米的篱笆围成,若墙长为18米,设这个苗圃垂直于墙的一边长为x米.
如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为30米的篱笆围成,若墙长为18米,设这个苗圃垂直于墙的一边长为x米. 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置,如果BC=2,那么线段BE的长度为$\sqrt{2}$.
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置,如果BC=2,那么线段BE的长度为$\sqrt{2}$.