题目内容
11.(1)先化简,并选一个自己喜欢的数代入求值.$\frac{2a+1}{{{a^2}-1}}•\frac{{{a^2}-2a+1}}{{{a^2}-a}}-\frac{1}{a+1}$(2)解不等式组:$\left\{\begin{array}{l}2x+5≤3(x+2)①\\ 3x-1<5②\end{array}$,并把它的解集表示在数轴上.
分析 (1)利用分解因式、通分等手段将原式进行化简,根据分式成立的意义找出a的取值范围,任取一值将其代入化简后的算式即可得出结论;
(2)分别解出不等式组中的两不等式,由此得出x的取值范围,再根据在数轴上标示不等式的解集的方法将其在数轴上表示出来.
解答 解:(1)原式=$\frac{2a+1}{(a+1)(a-1)}$•$\frac{(a-1)^{2}}{a(a-1)}$-$\frac{1}{a+1}$,
=$\frac{2a+1}{a(a+1)}$-$\frac{a}{a(a+1)}$,
=$\frac{2a+1-a}{a(a+1)}$,
=$\frac{1}{a}$.
由(a2-1)(a2-a)(a+1)≠0,可知:
a≠0,a≠±1.
将a=2代入$\frac{1}{a}$得:
原式=$\frac{1}{2}$.
(2)解①得:x≥-1;解②得:x<2.
故不等式组$\left\{\begin{array}{l}2x+5≤3(x+2)①\\ 3x-1<5②\end{array}$的解集为-1≤x<2.
将-1≤x<2在数轴上表示出来如下图.
点评 本题考查了分式的化简求值、在数轴上标示不等式的解集以及解一元一次不等式组,解题的关键是:(1)将原等式进行化简;(2)解不等式得出x的取值范围.本题属于基础题,难度不大,解决该题型题目时,先化简再求值是关键(要注意分式成立的条件).

练习册系列答案
相关题目
19.若分式$\frac{{{x^2}-x-2}}{x+1}$的值为0,则x的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
3.下列命题为假命题的是( )
| A. | 对顶角相等 | B. | 两直线平行,同位角相等 | ||
| C. | 内错角相等 | D. | 三角形内角和是180度 |
20.下列调查中,适合用普查(全面调查)方式的是( )
| A. | 了解我县流动人口数量 | |
| B. | 了解某班学生的视力情况 | |
| C. | 了解江苏卫视“非诚勿扰”节目的收视率 | |
| D. | 了解一批炮弹的杀伤半径 |
 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=2cm,试求出AE的长度.
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=2cm,试求出AE的长度. 如图,在△ABC中,AD是中线,G是重心,AD=6,则DG=2.
如图,在△ABC中,AD是中线,G是重心,AD=6,则DG=2.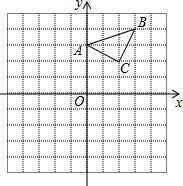 已知:在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
已知:在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)