题目内容
6.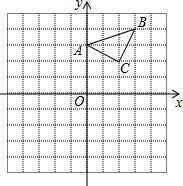 已知:在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
已知:在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)(1)画出△ABC向下平移6个单位,再向右平移一个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2:1;
(3)求出△A2BC2的面积.
分析 (1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用位似图形的性质得出对应点位置进而得出答案;
(3)直接利用等腰直角三角形的性质求出△A2BC2的面积.
解答 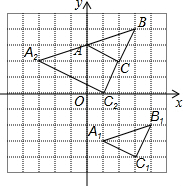 解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
C1(3,-4);
(2)如图所示:△A2BC2,即为所求;
(3)由图形可得:△A2BC2是等腰直角三角形,且A2C2=BC2=2$\sqrt{5}$,
故△A2BC2的面积为:$\frac{1}{2}$×2$\sqrt{5}$×2$\sqrt{5}$=10.
点评 此题主要考查了位似变换以及平移变换和三角形面积求法,正确得出对应点位置是解题关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
17.若两个相似三角形的周长比为1:3,则面积比为( )
| A. | 1:3 | B. | 3:1 | C. | 1:9 | D. | 9:1 |
14.下列说法:
①两负数比较大小,绝对值大的反而小;
②数轴上,在原点左边离原点越近的数越小;
③所有的有理数都可以用数轴上的点表示;
④倒数等于它本身的数是1或0;
⑤两数相加,和一定大于任何一个加数.
其中正确的有( )
①两负数比较大小,绝对值大的反而小;
②数轴上,在原点左边离原点越近的数越小;
③所有的有理数都可以用数轴上的点表示;
④倒数等于它本身的数是1或0;
⑤两数相加,和一定大于任何一个加数.
其中正确的有( )
| A. | ①④ | B. | ②③④ | C. | ①③ | D. | ①②③④ |
15.函数$y=\frac{{\sqrt{x-2}}}{x-4}$的自变量的取值范围是( )
| A. | x≥2 | B. | x≥2且x≠4 | C. | x>2且x≠4 | D. | x≠4 |
16.下列长度的三条线段,能组成三角形的是( )
| A. | 1,2,3 | B. | 4,5,10 | C. | 7,8,9 | D. | 9,10,20 |
 如图,在平面直角坐标系xOy中,A(-1,5),B(-2,0),C(-4,3).
如图,在平面直角坐标系xOy中,A(-1,5),B(-2,0),C(-4,3). 有一张图纸被损坏,但上面有如图所示的两个标志点A(-3,1),B(-3,-3)可见,而主要建筑C(3,2)破损,
有一张图纸被损坏,但上面有如图所示的两个标志点A(-3,1),B(-3,-3)可见,而主要建筑C(3,2)破损,