题目内容
17.点A(0,-3),点B(0,-4),点C在x轴上,如果△ABC的面积为15,则点C的坐标是(30,0)或(-30,0).分析 根据A、B两点特点,求出线段AB的长度,根据C点特征设出C点坐标,然后利用面积列出一个方程,从而求得点C的坐标.
解答 解:∵点A(0,-3),点B(0,-4),
∴AB=1
∵点C在x轴上,
设C(x,0),
∵△ABC的面积为15,
∴$\frac{1}{2}$×AB×|x|=15,
即:$\frac{1}{2}$×1×|x|=15
解得:x=±30
∴点C坐标是:(30,0),(-30,0).
故答案为:(30,0),(-30,0).
点评 题目考查了平面直角坐标系点的坐标和图形的性质,通过对三角形的面积求解,求出相关点的坐标.题目整体较为简单,需要注意的是不要出现漏解现象.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
3.在直角三角形ABC中,已知∠C=90°,∠A=60°,AC=10$\sqrt{3}$,则BC等于( )
| A. | 30 | B. | 10 | C. | 20 | D. | 5$\sqrt{3}$ |
2.在平面直角坐标系中,点P(-2,5)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
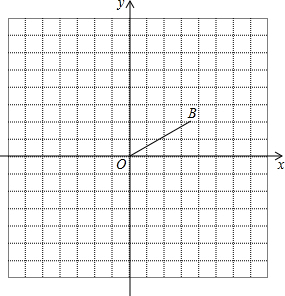 如图,在平面直角坐标系中,点B的坐标是(2$\sqrt{3}$,2),将线段OB绕点O顺时针旋转120°,点B的对应点是点B.
如图,在平面直角坐标系中,点B的坐标是(2$\sqrt{3}$,2),将线段OB绕点O顺时针旋转120°,点B的对应点是点B. →装入不透明的甲袋
→装入不透明的甲袋 →装入不透明的乙袋,李南从甲袋中,王易从乙袋中,各自随机地摸出一个球(不放回),把李南摸出的球的编号作为横坐标x,把王易摸出的球的编号作为纵坐标y,用列表法或画树状图法表示出(x,y)的所有可能出现的结果;
→装入不透明的乙袋,李南从甲袋中,王易从乙袋中,各自随机地摸出一个球(不放回),把李南摸出的球的编号作为横坐标x,把王易摸出的球的编号作为纵坐标y,用列表法或画树状图法表示出(x,y)的所有可能出现的结果;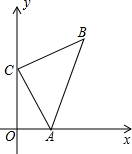 如图,A(3,0),C(0,6),AC⊥BC,且AC=BC,求点B的坐标.
如图,A(3,0),C(0,6),AC⊥BC,且AC=BC,求点B的坐标.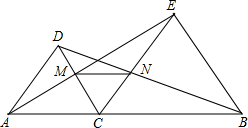 已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.