题目内容
3.在直角三角形ABC中,已知∠C=90°,∠A=60°,AC=10$\sqrt{3}$,则BC等于( )| A. | 30 | B. | 10 | C. | 20 | D. | 5$\sqrt{3}$ |
分析 先求出∠B=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得AB=2AC,然后利用勾股定理求出BC即可.
解答  解:∵∠C=90°,∠A=60°,
解:∵∠C=90°,∠A=60°,
∴∠B=90°-60°=30°,
∴AB=2AC=20$\sqrt{3}$,
由勾股定理得:BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{(20\sqrt{3})^{2}-(10\sqrt{3})^{2}}$=30.
故选:A.
点评 本题考查了直角三角形30°角所对的直角边等于斜边的一半、勾股定理;熟练掌握勾股定理,由直角三角形30°角所对的直角边等于斜边的一半求出AB是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点P(-1,1),则k的值是( )
| A. | 0 | B. | -2 | C. | 2 | D. | -1 |
8. 某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为200人,表中m的值为90;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
 某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 50 | m | 40 | 20 |
(1)本次问卷调查共抽取的学生数为200人,表中m的值为90;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
18. 如图是一个“中”的几何体,则该几何体的俯视图为( )
如图是一个“中”的几何体,则该几何体的俯视图为( )
 如图是一个“中”的几何体,则该几何体的俯视图为( )
如图是一个“中”的几何体,则该几何体的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
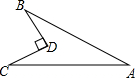 如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积.
如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积.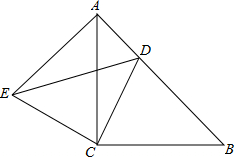 如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.
如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.