题目内容
12.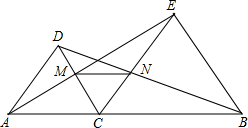 已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.(1)求证:△ACE≌△DCB;
(2)求证:MN∥AB.
分析 (1)根据等边三角形的性质可以得出AC=DC,BC=EC,∠ACD=∠BCE=60°,就可以求出∠ACE=∠DCB=120°,由边角边就可以得出△ACE≌△DCB;
(2)根据全等三角形的性质得到AE=DB,∠EAC=∠BDC,推出△ACM≌△DCN(ASA),由全等三角形的性质得到CM=CN证得△CMN为等边三角形,于是得到∠MNC=∠ECB=60°,根据平行线的判定即可得到结论.
解答 解:(1)∵△ACD和△BCE是等边三角形,
∴AC=DC,BC=EC,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB.
在△ACE和△DCB中
$\left\{\begin{array}{l}{AC=DC}\\{∠ACE=∠DCB}\\{CE=CB}\end{array}\right.$,
∴△ACE≌△DCB(SAS);
(2)∵△ACE≌△DCB(SAS),
∴AE=DB,∠EAC=∠BDC,
∵∠ACD=∠ECB=60°,
∴∠DCE=60°,
在△ACM和△DCN中,
$\left\{\begin{array}{l}{∠CAM=∠CDN}\\{AC=DC}\\{∠ACM=∠DCN}\end{array}\right.$,
∴△ACM≌△DCN(ASA),
∴CM=CN,
∴△CMN为等边三角形,
∴∠MNC=∠ECB=60°,
∴MN∥AB.
点评 本题考查了等边三角形的判定及性质的运用,全等三角形的判定及性质的运用,平行线的判定的运用,解答时证明三角形全等是关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
18.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点P(-1,1),则k的值是( )
| A. | 0 | B. | -2 | C. | 2 | D. | -1 |
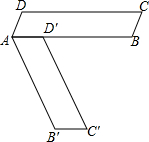 将?ABCD(如图)绕点A旋转后,点D落在边AB上的点D′,点C落到C′,且点C′、B、C在一直线上.如果AB=13,AD=3,那么∠A的余弦值为$\frac{5}{13}$.
将?ABCD(如图)绕点A旋转后,点D落在边AB上的点D′,点C落到C′,且点C′、B、C在一直线上.如果AB=13,AD=3,那么∠A的余弦值为$\frac{5}{13}$.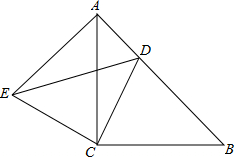 如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.
如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.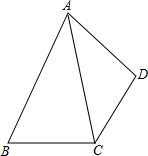 如图,AC平分∠BAD,CD=CB,AB>AD,求证:∠B+∠ADC=180°.
如图,AC平分∠BAD,CD=CB,AB>AD,求证:∠B+∠ADC=180°. 如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.
如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.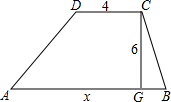 如图,梯形ABCD上底的长是4,下底的长是x,高是6.
如图,梯形ABCD上底的长是4,下底的长是x,高是6.