题目内容
2.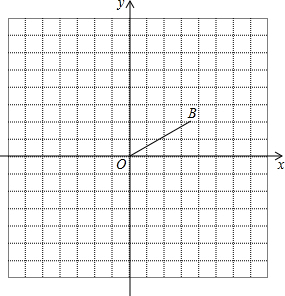 如图,在平面直角坐标系中,点B的坐标是(2$\sqrt{3}$,2),将线段OB绕点O顺时针旋转120°,点B的对应点是点B.
如图,在平面直角坐标系中,点B的坐标是(2$\sqrt{3}$,2),将线段OB绕点O顺时针旋转120°,点B的对应点是点B.(1)①求点B绕点O旋转到点B1所经过的路程长;
②在图中画出$\widehat{B{B}_{1}}$,并直接写出点B1的坐标是(0,-4);
(2)有7个球除了编号不同外,其他均相同,李南和王易设计了如下的一个规则:
 →装入不透明的甲袋
→装入不透明的甲袋 →装入不透明的乙袋,李南从甲袋中,王易从乙袋中,各自随机地摸出一个球(不放回),把李南摸出的球的编号作为横坐标x,把王易摸出的球的编号作为纵坐标y,用列表法或画树状图法表示出(x,y)的所有可能出现的结果;
→装入不透明的乙袋,李南从甲袋中,王易从乙袋中,各自随机地摸出一个球(不放回),把李南摸出的球的编号作为横坐标x,把王易摸出的球的编号作为纵坐标y,用列表法或画树状图法表示出(x,y)的所有可能出现的结果;(3)李南和王易各取一次小球所确定的点(x,y)落在$\widehat{B{B}_{1}}$上的概率是$\frac{1}{6}$.
分析 (1)①先利用勾股定理计算出OB,然后根据弧长公式计算点B绕点O旋转到点B1所经过的路程长;
②由①得∠BOH=30°,则线段OB绕点O顺时针旋转120°,点B的对应点是点B1在y轴的负半轴上,于是可得到$\widehat{B{B}_{1}}$,再写出点B1的坐标;
(2)利用树状图展示所有12种等可能的结果数;
(3)计算各点到原点的距离可判断点(x,y)落在$\widehat{B{B}_{1}}$上的结果数为2,然后根据概率公式求解.
解答 解:(1)①作BH⊥x轴于点H,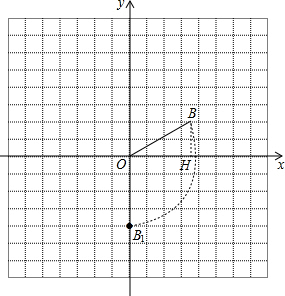
∵点B的坐标是(2$\sqrt{3}$,2),
∴BH=2,OH=2$\sqrt{3}$,
∴OB=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4,
∴B绕点O旋转到点B1所经过的路程长=$\frac{120•π•4}{180}$=$\frac{8π}{3}$;
②如图,$\widehat{B{B}_{1}}$为所作,点B1的坐标是(0,-4);
(2)画树状图为:
共有12种等可能的结果数;
(3)点(x,y)落在$\widehat{B{B}_{1}}$上的结果数为2,
所以点(x,y)落在$\widehat{B{B}_{1}}$上的概率=$\frac{2}{12}$=$\frac{1}{6}$.
故答案为(0,-4),$\frac{1}{6}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了弧长公式和树状图法.

练习册系列答案
相关题目
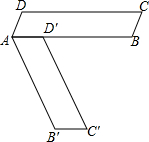 将?ABCD(如图)绕点A旋转后,点D落在边AB上的点D′,点C落到C′,且点C′、B、C在一直线上.如果AB=13,AD=3,那么∠A的余弦值为$\frac{5}{13}$.
将?ABCD(如图)绕点A旋转后,点D落在边AB上的点D′,点C落到C′,且点C′、B、C在一直线上.如果AB=13,AD=3,那么∠A的余弦值为$\frac{5}{13}$.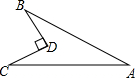 如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积.
如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积.