题目内容
9.在Rt△ABC中,∠C=90°,AC=1,AB=2,则sinA=$\frac{\sqrt{3}}{2}$.分析 根据勾股定理求出BC的长,根据锐角的正弦为对边比斜边计算即可.
解答 解:∵∠C=90°,AC=1,AB=2,
∴BC=$\sqrt{3}$,
则sinA=$\frac{BC}{AB}$=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查的是锐角三角函数的定义,掌握在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边是解题的关键.

练习册系列答案
相关题目
18. 如图是一个“中”的几何体,则该几何体的俯视图为( )
如图是一个“中”的几何体,则该几何体的俯视图为( )
 如图是一个“中”的几何体,则该几何体的俯视图为( )
如图是一个“中”的几何体,则该几何体的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
19. 如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )
如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )
 如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )
如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )| A. | 14° | B. | 28° | C. | 32° | D. | 40° |
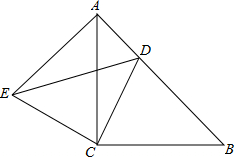 如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.
如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点. 如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.
如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO. 将两块直角三角尺的直角顶点重合为如图的位置,若∠AOC=20°,则∠BOD=20°.
将两块直角三角尺的直角顶点重合为如图的位置,若∠AOC=20°,则∠BOD=20°.