题目内容
7.已知点P(a,b)在直线y=-x+8上,且$\sqrt{ab-15}$=0,则点P到原点O的距离等于$\sqrt{34}$.分析 根据题意得出a+b=8,ab=15,然后根据勾股定理即可求得.
解答 解:∵点P(a,b)在直线y=-x+8上,
∴b=-a+8,
∴a+b=8,
∵$\sqrt{ab-15}$=0,
∴ab=15,
点P到原点O的距离为:$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{(a+b)^{2}-2ab}$=$\sqrt{{8}^{2}-2×15}$=$\sqrt{34}$,
故答案为$\sqrt{34}$.
点评 本题考查了一次函数图象上点的坐标特征以及勾股定理的应用,根据题意得出a+b=8,ab=15是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
18. 如图是一个“中”的几何体,则该几何体的俯视图为( )
如图是一个“中”的几何体,则该几何体的俯视图为( )
 如图是一个“中”的几何体,则该几何体的俯视图为( )
如图是一个“中”的几何体,则该几何体的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
19. 如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )
如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )
 如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )
如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )| A. | 14° | B. | 28° | C. | 32° | D. | 40° |
16.下列说法不正确的是( )
| A. | 1的平方根是±1 | B. | 1的立方根是1 | C. | 2是$\sqrt{4}$的平方根 | D. | -$\root{3}{3}$是-3的立方根 |
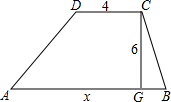 如图,梯形ABCD上底的长是4,下底的长是x,高是6.
如图,梯形ABCD上底的长是4,下底的长是x,高是6.