题目内容
5.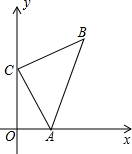 如图,A(3,0),C(0,6),AC⊥BC,且AC=BC,求点B的坐标.
如图,A(3,0),C(0,6),AC⊥BC,且AC=BC,求点B的坐标.
分析 作BD⊥y轴于点D,易证∠CBD=∠ACO,由AAS证明△CDB≌△AOC,得出对应边相等,即可得出结果.
解答 解:作BD⊥y轴于点D,如图所示: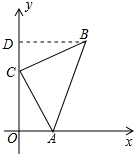
则∠BDC=90°,
∴∠CBD+∠DCB=90°,
∵A(3,0),C(0,6),
∴OA=3,OC=6,
∵AC⊥BC,
∴∠DCB+∠ACO=90°,
∴∠CBD=∠ACO,
在△CDB和△AOC中,
$\left\{\begin{array}{l}{∠BDC=∠COA=90°}&{\;}\\{∠CBD=∠ACO}&{\;}\\{BC=CA}&{\;}\end{array}\right.$,
∴△CDB≌△AOC(AAS),
∴BD=OC=6,CD=OA=3,
∴OD=OC+CD=9,
∴点B坐标为(6,9).
点评 本题考查了全等三角形的判定与性质、坐标与图形性质;熟练掌握坐标与图形性质,证明三角形全等得出对应边相等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为200人,表中m的值为90;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
 某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 50 | m | 40 | 20 |
(1)本次问卷调查共抽取的学生数为200人,表中m的值为90;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
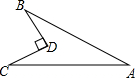 如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积.
如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积.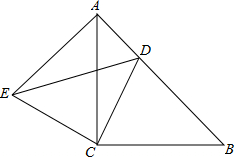 如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.
如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.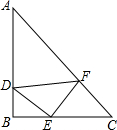 如图,△ABC,△DEF都是等腰直角三角形,D、E、F分别在AB、BC、CA上,已知∠B=∠DEF=90°,AB=BC,DE=EF.
如图,△ABC,△DEF都是等腰直角三角形,D、E、F分别在AB、BC、CA上,已知∠B=∠DEF=90°,AB=BC,DE=EF. 将两块直角三角尺的直角顶点重合为如图的位置,若∠AOC=20°,则∠BOD=20°.
将两块直角三角尺的直角顶点重合为如图的位置,若∠AOC=20°,则∠BOD=20°.