题目内容
17.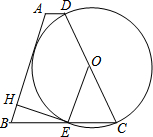 如图,梯形ABCD是等腰梯形,且AD∥BC,O是腰CD的中点,以CD长为直径作圆,交BC于E,过E作EH⊥AB于H.
如图,梯形ABCD是等腰梯形,且AD∥BC,O是腰CD的中点,以CD长为直径作圆,交BC于E,过E作EH⊥AB于H.(1)求证:OE∥AB;
(2)若EH=$\frac{1}{2}$CD,求证:AB是⊙O的切线;
(3)在(2)的条件下,若BE=4BH,求$\frac{BH}{CE}$的值.
分析 (1)根据等腰梯形的性质、等腰三角形的性质可以判断出∠B=∠OEC,然后由同位角相等得出OE∥AB;
(2)作辅助线(过点O作OF⊥AB于点F,过点O作OG∥BC交AB于点G)构建平行四边形OEHF,然后由“平行四边形的对边相等的性质”、由已知条件求得OF=EH=$\frac{1}{2}$CD,即OF是⊙O的半径;最后根据切线的判定得出结论;
(3)求出△EHB∽△DEC,根据相似三角形的性质和勾股定理解答.
解答 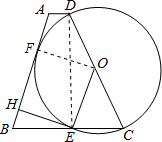 (1)证明:∵四边形ABCD是等腰梯形,且AD∥BC,
(1)证明:∵四边形ABCD是等腰梯形,且AD∥BC,
∴AB=CD,∠B=∠C;
又∵CD是直径,点O是腰CD的中点,
∴点O是圆心,
∴OE=OC,
∴∠OEC=∠C(等边对等角),
∴∠OEC=∠B(等量代换),
∴OE∥AB(同位角相等,两直线平行);
(2)证明:过点O作OF⊥AB于点F.
∵由(1)知,OE∥AB,
∴OE∥FH;
又∵EH⊥AB,
∴FO∥HE,
∴四边形OEHF是平行四边形(有两组对边平行的四边形是平行四边形),
∴OF=EH(平行四边形的对边相等);
∵EH=$\frac{1}{2}$CD,
∴OF=$\frac{1}{2}$CD,即OF是⊙O的半径,
∴AB是⊙O的切线;
(3)解:连接DE.
∵CD是直径,
∴∠DEC=90°(直径所对的圆周角是直角),则∠DEC=∠EHB,
又∵∠B=∠C,
∴△EHB∽△DEC,
∴$\frac{BH}{CE}$=$\frac{BE}{CD}$,
∵BE=4BH,
∴设BH=k,则BE=4k,EH=$\sqrt{B{E}^{2}-B{H}^{2}}$=$\sqrt{15}$k;
∴CD=2EH=2$\sqrt{15}$k
∴$\frac{BH}{CE}$=$\frac{BE}{CD}$=$\frac{4k}{2\sqrt{15}k}$=$\frac{2\sqrt{15}}{15}$.
点评 本题考查了圆的切线性质,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形、矩形解决有关问题.

 阅读快车系列答案
阅读快车系列答案
| A. | 78个 | B. | 99个 | C. | 105个 | D. | 121个 |
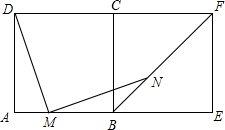 如图,正方形ABCD和正方形BEFC,M是AB上一动点,从A至B移动(不与A、B重合),DM⊥MN,交对角线BF于点N,探究DM和MN之间的数量关系,并加以证明.
如图,正方形ABCD和正方形BEFC,M是AB上一动点,从A至B移动(不与A、B重合),DM⊥MN,交对角线BF于点N,探究DM和MN之间的数量关系,并加以证明.