题目内容
7.学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的1.5倍;用600元单独购买甲种图书比单独购买乙种图书要少10本.(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书共40本,其中甲种图书a本,投入的经费为W元,
①请写出W关于a的函数关系式;
②若投入的经费不超过1050元,且使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?并求出最节省的购买方案和最节省经费;
(3)若学校计划购买这两种图书总数超过30本,其中甲种图书a本,乙种图书b本,且投入的经费恰好为690元,则b=24,27(写出两种可能的值).
分析 (1)总费用除以单价即为数量,设乙种图书的单价为x元,则甲种图书的单价为1.5x元,根据两种图书数量之间的关系列方程;
(2)设购进甲种图书a本,则购进乙种图书(40-a)本,①根据总费用等于购买的甲种图书的费用+购买的甲种图书的费用即可求得函数关系式;②根据“投入的经费不超过1050元,甲种图书数量不少于乙种图书的数量”列出不等式组解决问题.
(3)根据题意得$\left\{\begin{array}{l}{30a+20b=690①}\\{a+b>30②}\end{array}\right.$,由①得a=$\frac{69-2b}{3}$=23-$\frac{2}{3}$b,代入②解得b>21,因为a、b都是整数,即可求得b的取值.
解答 解:(1)设乙种图书的单价为x元,则甲种图书的单价为1.5x元,由题意得$\frac{600}{x}$-$\frac{600}{1.5x}$=10
解得:x=20
则1.5x=30,
经检验得出:x=20是原方程的根,
答:甲种图书的单价为30元,乙种图书的单价为20元;
(2)①设购进甲种图书a本,则购进乙种图书(40-a)本,根据题意得:
W=30a+20(40-a)=800+10a,
即W=10a+800;
②$\left\{\begin{array}{l}{10a+800≤1050}\\{a≥40-a}\end{array}\right.$
解得:20≤a≤25,
所以a=20、21、22、23、24、25,则40-a=20、19、18、17、16、15
∴共有6种方案;
由W=10a+800可知:
当a取最小值时,W最小,
∴a=20,W最小=1000元;
(3)根据题意得$\left\{\begin{array}{l}{30a+20b=690①}\\{a+b>30②}\end{array}\right.$,
由①得a=$\frac{69-2b}{3}$=23-$\frac{2}{3}$b,
代入②解得b>21,
∵a、b都是整数,
∴b必须是3的倍数,
∴b=24,27,30,33.
故答案为24,27.
点评 此题考查一次函数的应用,分式方程的运用,一元一次不等式组的运用,理解题意,抓住题目蕴含的数量关系是解决问题的关键.

| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
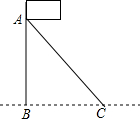 如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )| A. | 6sin50° | B. | 6cos50° | C. | $\frac{6}{sin50°}$ | D. | $\frac{6}{cos50°}$ |
| A. | 9,8 | B. | 9,7 | C. | 8,9 | D. | 9,9 |
| A. | a3•a2=a6 | B. | (a2)2=a4 | C. | (-3a)3=-9a3 | D. | a4+a5=a9 |
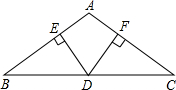 在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.
在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.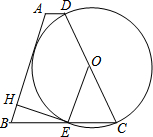 如图,梯形ABCD是等腰梯形,且AD∥BC,O是腰CD的中点,以CD长为直径作圆,交BC于E,过E作EH⊥AB于H.
如图,梯形ABCD是等腰梯形,且AD∥BC,O是腰CD的中点,以CD长为直径作圆,交BC于E,过E作EH⊥AB于H.