题目内容
8.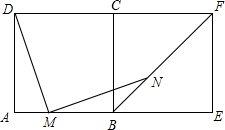 如图,正方形ABCD和正方形BEFC,M是AB上一动点,从A至B移动(不与A、B重合),DM⊥MN,交对角线BF于点N,探究DM和MN之间的数量关系,并加以证明.
如图,正方形ABCD和正方形BEFC,M是AB上一动点,从A至B移动(不与A、B重合),DM⊥MN,交对角线BF于点N,探究DM和MN之间的数量关系,并加以证明.
分析 DM=MN,在AD上取AP=AM,连接DM,证明△DPM≌△MBN即可证明DM=MN.
解答 解:DM=MN,
在AD上取AP=AM,连接DM,
∵四边形ABCD是正方形,
∴AB=AD,
∴DP=MB,
∵DM⊥MN,∠A=90°,
∴∠ADM+∠AMD=∠BMN+∠AMD=90°,
∴∠ADM=∠BMN,
∵AP=AM,
∴∠APM=45°,
∴∠DPM=135°,
∵BF是正方形CBEF的对角线,
∴∠CBF=45°,
∴∠MBN=135°,
∴∠DPM=∠MBN,
在△DPM和△MBN中
$\left\{\begin{array}{l}{∠DPM=∠MBN}\\{DP=MB}\\{∠ADM=∠BMN}\end{array}\right.$,
∴△DPM≌△MBN,
∴DM=MN.
点评 本题主要考查了全等三角形的判定与性质以及正方形的性质,通过辅助线构造全等三角形是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
19.一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9,这五个数据的众数和中位数分别是( )
| A. | 9,8 | B. | 9,7 | C. | 8,9 | D. | 9,9 |
16.下列运算正确的是( )
| A. | a3•a2=a6 | B. | (a2)2=a4 | C. | (-3a)3=-9a3 | D. | a4+a5=a9 |
13.下列不是分解因式的是( )
| A. | 10a2b+6ab2=2ab(5a+3b) | B. | (2x+y)(x-y)=2x2-xy-y2 | ||
| C. | y2-9z2=(y+3z)(y-3z) | D. | m2n2-2mna+a2=(mn-a)2 |
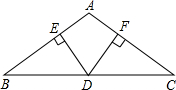 在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.
在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.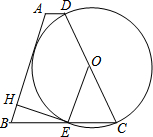 如图,梯形ABCD是等腰梯形,且AD∥BC,O是腰CD的中点,以CD长为直径作圆,交BC于E,过E作EH⊥AB于H.
如图,梯形ABCD是等腰梯形,且AD∥BC,O是腰CD的中点,以CD长为直径作圆,交BC于E,过E作EH⊥AB于H.