题目内容
17．若平行四边形中两个内角的度数比为1：2，则其中较大的内角是（ ）| A． | 45° | B． | 60° | C． | 90° | D． | 120° |
分析 据平行四边形的性质得出AB∥CD，推出∠B+∠C=180°，根据∠B：∠C=1：2，求出∠C即可．
解答 解：∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠B+∠C=180°，
∵∠B：∠C=1：2，
∴∠C=$\frac{2}{3}$×180°=120°，
故选D．
点评 本题考查了平行线的性质和平行四边形的性质的应用，能熟练地运用性质进行计算是解此题的关键，题目比较典型，难度不大．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
8．下列各式中，属于最简二次根式的是（ ）
| A． | $\sqrt{4}$ | B． | $\sqrt{\frac{1}{5}}$ | C． | $\sqrt{6}$ | D． | $\sqrt{8}$ |
9．
如图，平行四边形ABCD的对角线交于点O，且AB=8，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是（ ）
如图，平行四边形ABCD的对角线交于点O，且AB=8，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是（ ）| A． | 15 | B． | 16 | C． | 30 | D． | 40 |
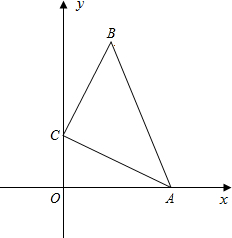如图，在直角坐标系中，△ABC满足∠BCA=90°，AC=BC=5$\sqrt{2}$，点A、C分别在x轴和y轴上，当点A从原点开始沿x轴的正方向运动时，则点C始终在y轴上运动，点B始终在第一象限运动．