题目内容
15.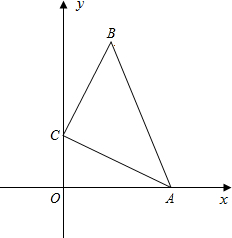 如图,在直角坐标系中,△ABC满足∠BCA=90°,AC=BC=5$\sqrt{2}$,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.
如图,在直角坐标系中,△ABC满足∠BCA=90°,AC=BC=5$\sqrt{2}$,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.(1)当AB∥y轴时,B点坐标是(5,10);
(2)随着A、C的运动,当点B落在直线y=3x上时,求此时A点的坐标;
(3)在(2)的条件下,在y轴上是否存在点D,使以O、A、B、D为顶点的四边形面积是40?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.
分析 (1)根据勾股定理,可得AB的长,根据勾股定理,可得CD的长,可得B点坐标;
(2)根据全等三角形的判定与性质,可得BE=OC=a,EC=OA=2a,根据勾股定理,可得a的长,可得A点坐标,
(3)分类讨论:①D在y轴的正半轴上;②D在y轴的负半轴上,根据面积的和差,可得关于b的方程,根据解方程,可得答案.
解答 解:(1)当AB∥y轴时,作CD⊥AB于D,如图1: ,
,
由勾股定理,得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
BD=AD=5,
由勾股定理,得
CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{(5\sqrt{2})^{2}-{5}^{2}}$=5
B点坐标是 (5,10).
(2)过点B作BE⊥y轴,如图2: ,
,
在△BCE和△COA中,
$\left\{\begin{array}{l}{∠E=∠O}\\{∠ECB=∠OAC}\\{BC=CA}\end{array}\right.$,
∴△BEC≌△COA(AAS)
∴BE=OC,EC=OA.
设点B(a,3a),
∴BE=a,OE=3a
∴BE=OC=a,EC=OA=2a,
在Rt△OCA中,由勾股定理,得OC2+OA2=AC2,即a2+4a2=50,
解得:$a=\sqrt{10}$,OA=2a=2$\sqrt{10}$,
∴A($2\sqrt{10}$,0);
(3)①D在y轴的正半轴上,设D(0,b),作BE⊥x轴于E点,如图3: ,
,
SOABD=SOEBD+SABE=$\frac{1}{2}$(b+3$\sqrt{10}$)×$\sqrt{10}$+$\frac{1}{2}$$\sqrt{10}$×3$\sqrt{10}$=40,
解得b=2$\sqrt{10}$,即D(0,2$\sqrt{10}$);
②D在y轴的负半轴上,设D(0,-b),如图4: ,
,
SOBAD=SOAB+SOAD=$\frac{1}{2}$×2$\sqrt{10}$×3$\sqrt{10}$+$\frac{1}{2}$×2$\sqrt{10}$b=40,
解得b=$\sqrt{10}$,D(0,-$\sqrt{10}$).
故D点坐标为(0,$2\sqrt{10}$)或(0,$-\sqrt{10}$).
点评 本题考查了一次函数综合题,(1)利用勾股定理是解题关键;(2)利用了全等三角形的判定与性质,勾股定理;(3)利用面积的和差得出关于b的方程是解题关键,注意分类讨论,以防遗漏.

 智能训练练测考系列答案
智能训练练测考系列答案| A. | 45° | B. | 60° | C. | 90° | D. | 120° |

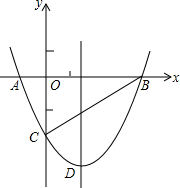 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).