题目内容
12.佳润商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示:| A | B | |
| 进价(万元/套) | 1.5 | 1.2 |
| 售价(万元/套) | 1.65 | 1.4 |
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
(3)在(2)的条件下,该商场所能获得的最大利润是多少万元?
分析 (1)设该商场计划购进A种品牌的教学设备x套,购进B种品牌的教学设备y套,根据购买两种设备共需66万元且全部销售后可获毛利润9万元,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设减少A种设备a套,则增加B种设备1.5a套,根据总价=单价×购进数量结合购进两种设备的总资金不超过69万元,即可得出关于a的一元一次不等式,解之即可得出a的取值范围,取其内的最大整数即可;
(3)设该商场获得的利润为w万元,根据总利润=单套利润×购进数量,即可得出w关于a的函数关系式,根据一次函数的性质结合a的取值范围即可解决最值问题.
解答 解:(1)设该商场计划购进A种品牌的教学设备x套,购进B种品牌的教学设备y套,
根据题意得:$\left\{\begin{array}{l}{1.5x+1.2y=66}\\{(1.65-1.5)x+(1.4-1.2)y=9}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=20}\\{y=30}\end{array}\right.$.
答:该商场计划购进A种品牌的教学设备20套,购进B种品牌的教学设备30套.
(2)设减少A种设备a套,则增加B种设备1.5a套,
根据题意得:1.5(20-a)+1.2(30+1.5a)≤69,
解得:a≤10.
答:A种设备购进数量至多减少10套.
(3)设该商场获得的利润为w万元,
根据题意得:w=(1.65-1.5)(20-a)+(1.4-1.2)(30+1.5a)=0.15a+9.
∵k=0.15>0,
∴w值随a值的增大而增大,
∴当a=10时,w取最大值,最大值为10.5.
答:在(2)的条件下,该商场所能获得的最大利润是10.5万元.
点评 本题考查了二元一次方程组的应用、一元一次不等式的应用、一次函数的性质以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据总价=单价×购进数量结合购进两种设备的总资金不超过69万元,找出关于a的一元一次不等式;(3)根据总利润=单套利润×购进数量,找出w关于a的函数关系式.

 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得△A1B1C1,且点A1落在边AB边上,取BB1的中点D,连接CD,则CD的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得△A1B1C1,且点A1落在边AB边上,取BB1的中点D,连接CD,则CD的长为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
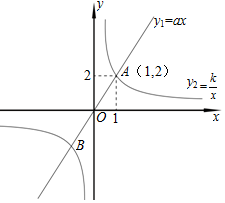 如图,已知正比例函数y1=ax的图象与反比例函数y2=$\frac{k}{x}$ 的图象有一个公共点A(1,2).
如图,已知正比例函数y1=ax的图象与反比例函数y2=$\frac{k}{x}$ 的图象有一个公共点A(1,2).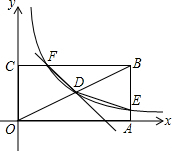 如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于点E,F,点B的坐标为(2$\sqrt{3}$,2).
如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于点E,F,点B的坐标为(2$\sqrt{3}$,2). 如图,在平面直角坐标系中,点A的坐标为(3,0),B为直线y=$\frac{\sqrt{3}}{3}$x上的一个动点,延长AB至C,使得AB=BC,过点C作CD⊥x轴于点D,交直线OB于点F,过点A作AE∥OB,交直线CD于点E.
如图,在平面直角坐标系中,点A的坐标为(3,0),B为直线y=$\frac{\sqrt{3}}{3}$x上的一个动点,延长AB至C,使得AB=BC,过点C作CD⊥x轴于点D,交直线OB于点F,过点A作AE∥OB,交直线CD于点E.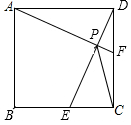 如图,正方形ABCD中,点E为BC的中点,作AF⊥DE交DE、DC分别于P、F点,连PC.
如图,正方形ABCD中,点E为BC的中点,作AF⊥DE交DE、DC分别于P、F点,连PC.